6 Modelos Univariados y Multivariados de Volatilidad
6.1 Motivación
En este capítulo discutiremos los modelos de Heterocedasticidad Condicional Autoregresiva (ARCH, por sus siglas en inglés) y modelos de Heterocedasticidad Condicional Autoregresiva Generalizados (GARCH, por sus siglas en inglés) tienen la característica de modelar situaciones como las que ilustra la Figura 6.2. Es decir:
Existen zonas donde la variación de los datos es mayor y zonas donde la variación es más estable–a estas situaciones se les conoce como de variabilidad por clúster–, y
los datos corresponden a innformación de alta frecuencia.
Iniciemos por las bibliotecas necesarias:
library(expm)
library(Matrix)
library(ggplot2)
library(quantmod)
library(moments)
library(dynlm)
library(broom)
library(FinTS)
library(lubridate)
library(forecast)
library(readxl)
library(MASS)
library(rugarch)
library(tsbox)
library(MTS)
library(rmgarch)
library(Rcpp)Para el análisis de temas financieros existe una librería de mucha utilidad llamada quantmod. En primer lugar esta librería permite acceder a datos financieros de un modo muy simple, es posible decargar series financieras desde yahoo, la FRED (Federal Reserve Economic Data), google, etc. Por otro lado, también es una librería que permite realizar gráficos altamente estéticos con unas cuantas líneas de código. Ahora, usaremos datos de Yahoo Finance respecto de la cotización del bitcoin (ticker: “BTC-USD”).
options("getSymbols.warning4.0"=FALSE)
BTC <-getSymbols("BTC-USD", src = "yahoo", auto.assign = FALSE)
BTC <- na.omit(BTC)
chartSeries(BTC,TA='addBBands();
addBBands(draw="p");
addVo();
addMACD()',# subset='2021',
theme="white")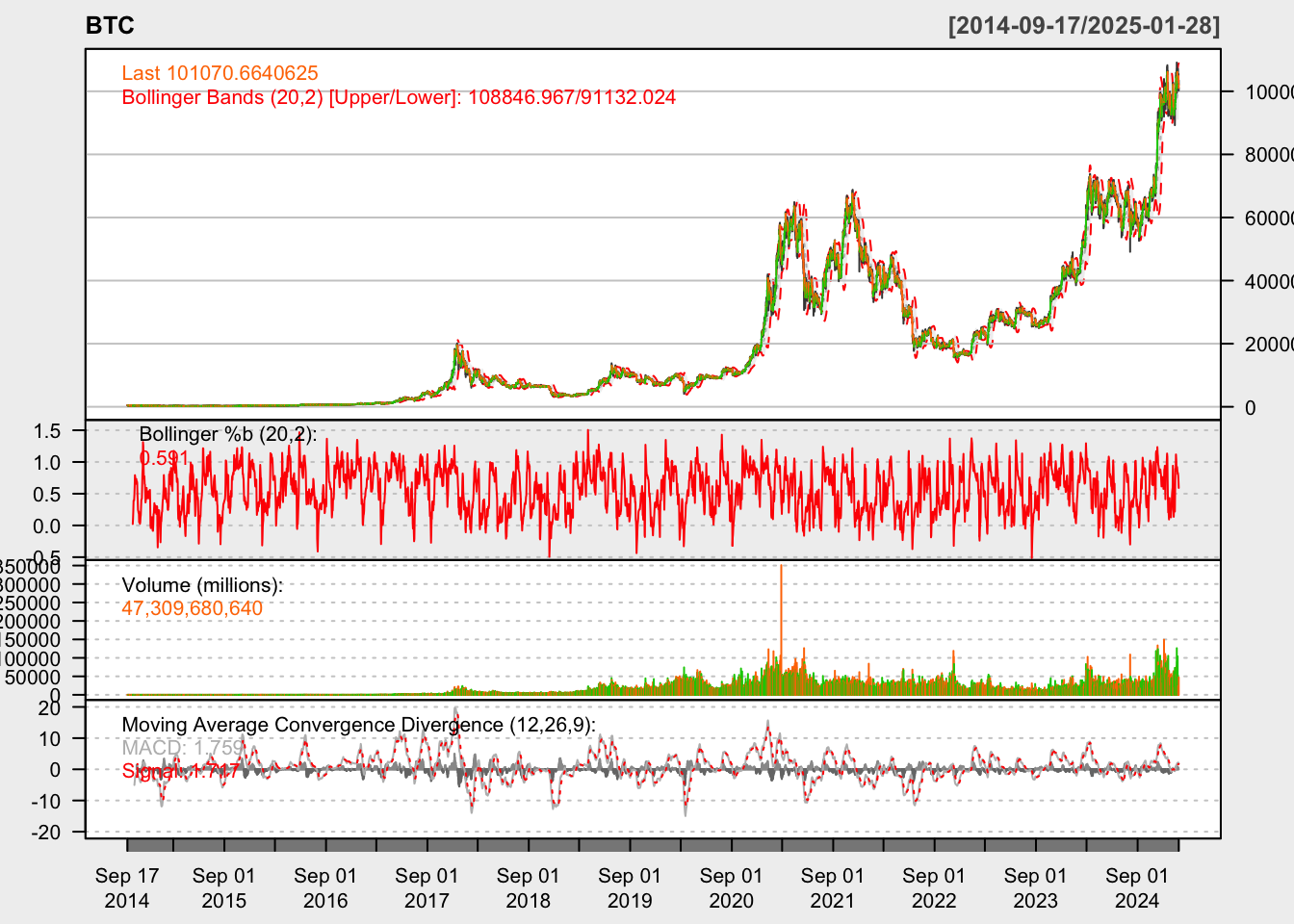
head(BTC)## BTC-USD.Open BTC-USD.High BTC-USD.Low BTC-USD.Close BTC-USD.Volume
## 2014-09-17 465.864 468.174 452.422 457.334 21056800
## 2014-09-18 456.860 456.860 413.104 424.440 34483200
## 2014-09-19 424.103 427.835 384.532 394.796 37919700
## 2014-09-20 394.673 423.296 389.883 408.904 36863600
## 2014-09-21 408.085 412.426 393.181 398.821 26580100
## 2014-09-22 399.100 406.916 397.130 402.152 24127600
## BTC-USD.Adjusted
## 2014-09-17 457.334
## 2014-09-18 424.440
## 2014-09-19 394.796
## 2014-09-20 408.904
## 2014-09-21 398.821
## 2014-09-22 402.152
tail(BTC)## BTC-USD.Open BTC-USD.High BTC-USD.Low BTC-USD.Close BTC-USD.Volume
## 2025-01-22 106136.4 106294.3 103360.3 103653.1 53878181052
## 2025-01-23 103657.7 106820.3 101257.8 103960.2 104104515428
## 2025-01-24 103965.7 107098.5 102772.1 104819.5 52388229265
## 2025-01-25 104824.0 105243.8 104120.4 104714.6 23888996502
## 2025-01-26 104713.2 105438.6 102507.7 102682.5 22543395879
## 2025-01-28 102097.5 103466.5 100265.7 101070.7 47309680640
## BTC-USD.Adjusted
## 2025-01-22 103653.1
## 2025-01-23 103960.2
## 2025-01-24 104819.5
## 2025-01-25 104714.6
## 2025-01-26 102682.5
## 2025-01-28 101070.7Para fines del ejercicio de esta clase, usaremos el valor de la acción ajustado. Esto nos servirá para calcular el rendimiento diario, o puesto en lenguaje de series temporales podemos decir que usaremos la serie en diferencias logarítmicas.
plot(BTC$`BTC-USD.Adjusted`)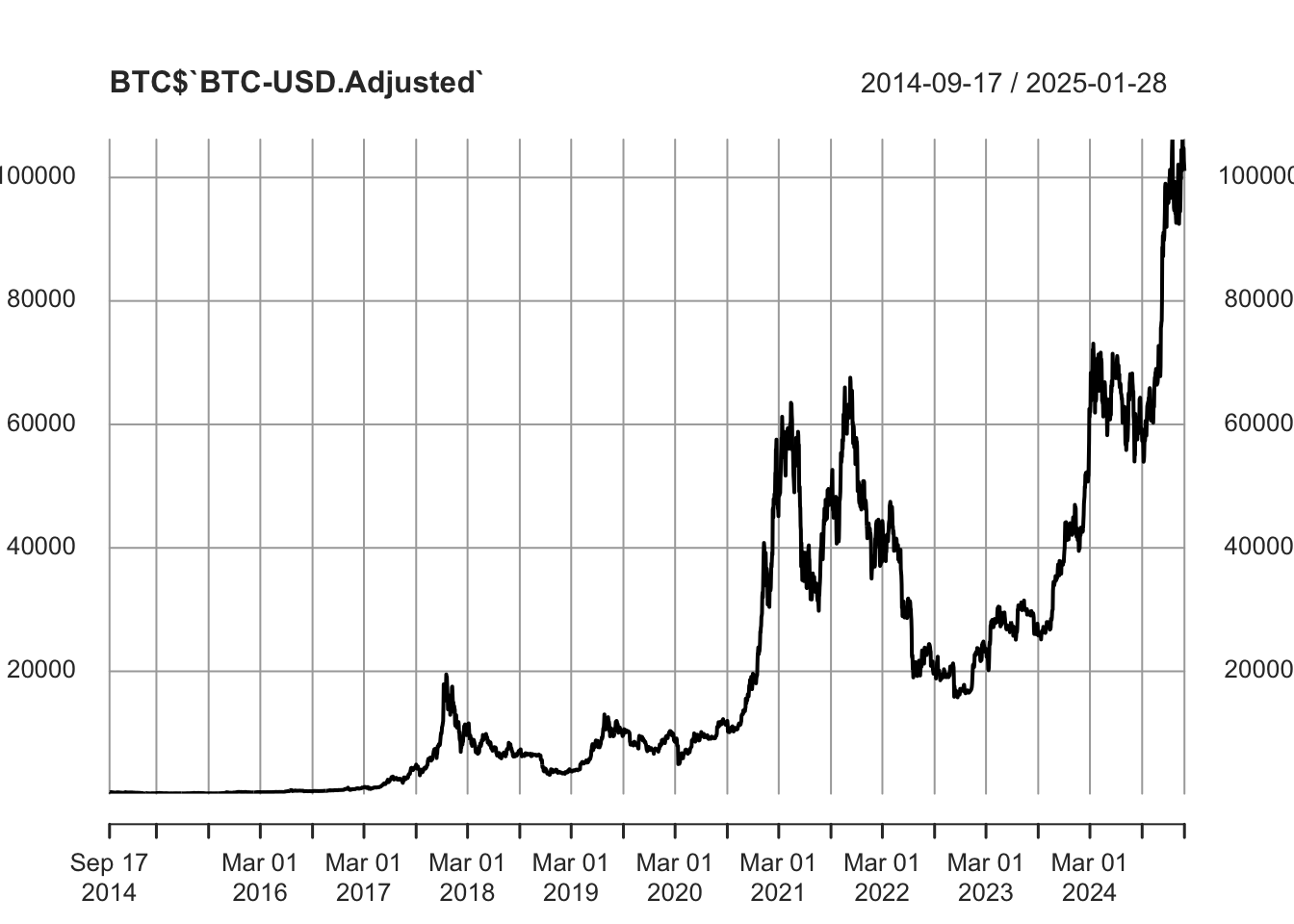
Figure 6.1: Evolución del precio del Bitcoin
Una de las preguntas relevantes al observar la serie en diferencias, es si podríamos afirmar que esta serie cumple con el supuesto de homoscedasticidad. Para ello, la Figura 6.2 muestra que las variaciones en el precio del Bitcoin muestran un escenario en el que no se cumple el supuesto de la homocedasticidad.
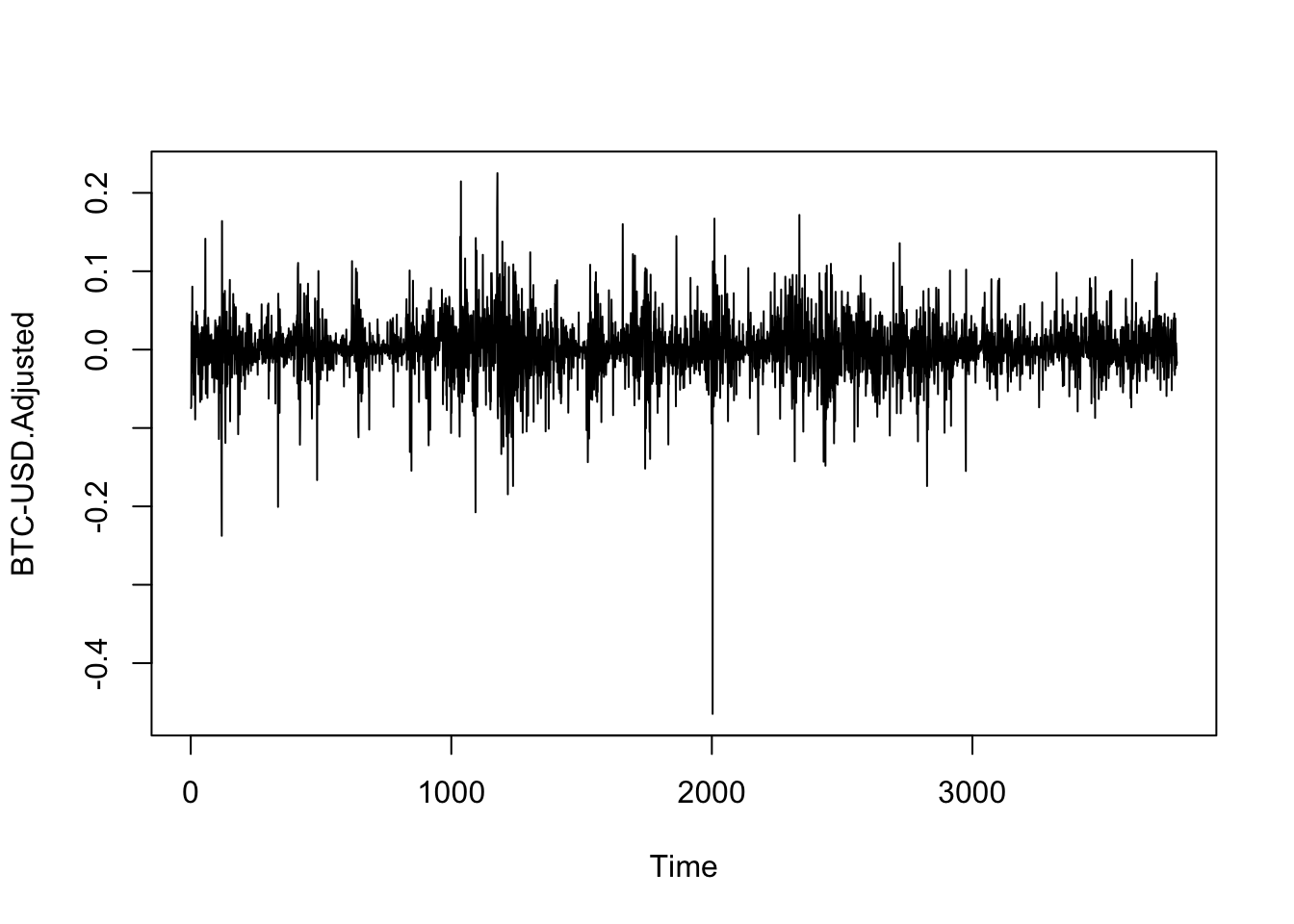
Figure 6.2: Evolución del rendimiento (diferenccias logarítmicas) del Bitcoin
6.1.1 Value at Risk (VaR)
Utilicemos como ejemplo el Valor en Riesgo. Este es básicamente es un cálculo que nos permite estimar el monto que una acción o portafolio podría perder dada una probabilidad \((1-\alpha)\). Supongamos un \(\alpha = 0.05\), de esta forma, la Figura 6.3 ilustra la región de la distribución que consideraríamos como el VaR.
## 5%
## -5.75
qplot(logret , geom = 'histogram') +
geom_histogram(fill = 'lightblue' , bins = 30) +
geom_histogram( aes(logret[logret < quantile(logret , 0.05)]) ,
fill = 'red' , bins = 30) +
labs(x = 'Daily Returns')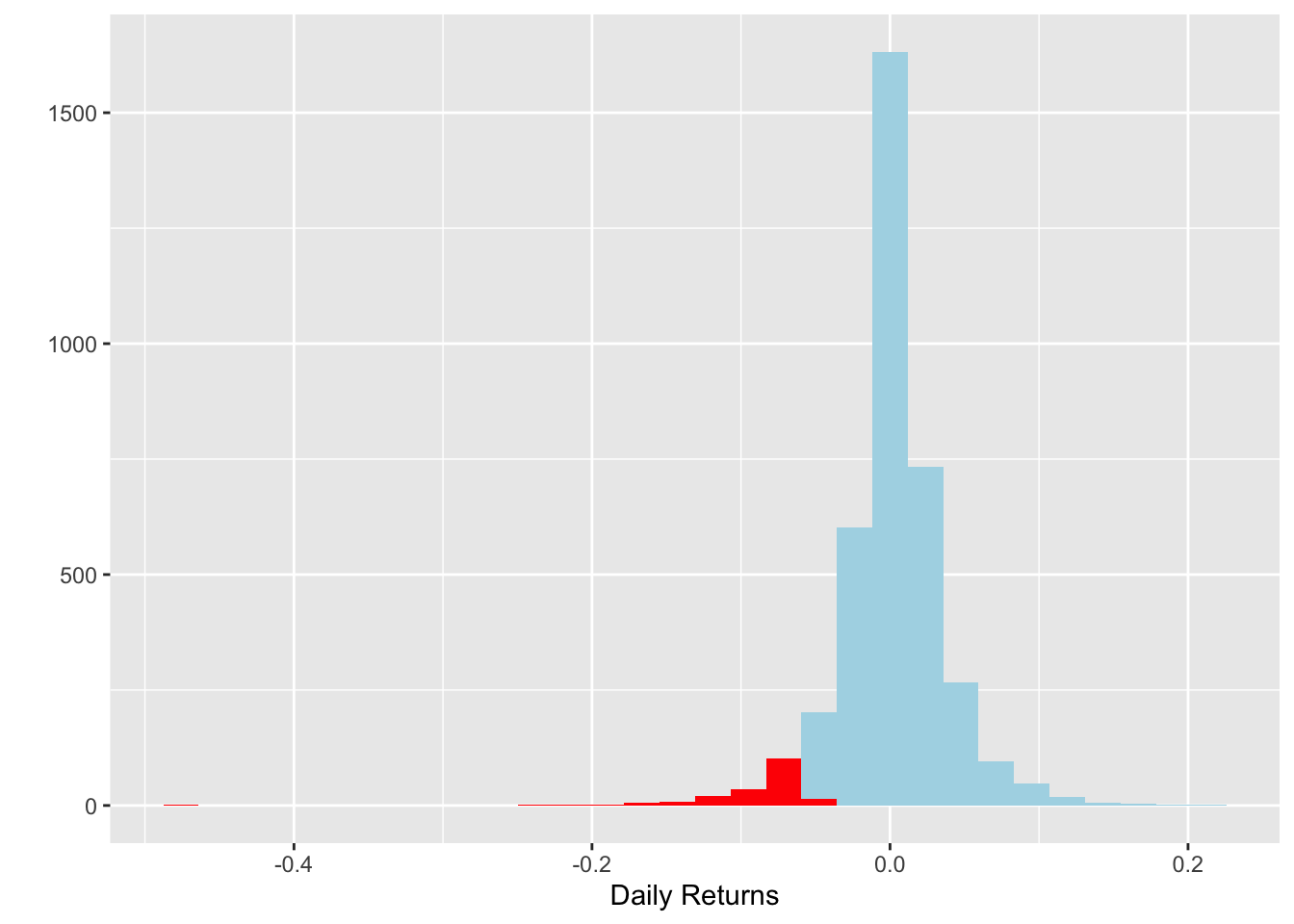
Figure 6.3: Histograma de rendimientos del Bitcoin
Ahora bien, una de las preguntas que nos podemos hacer es si los rendimientos del Bitcoin se aproximan a una distribución normal. Para ello, la Figura 6.4 ilustra esta comparación, de la cual podemos observar que una prueba de normalidad rechaza esa hipótesis–el estadístico Jarque-Bera indica que la serie de rendimientos no tiene una distribución normal–.
normal_dist <- rnorm(100000, mean(logret), sd(logret))
VaR_n <- quantile(normal_dist, 0.05)
ES_n <- mean(normal_dist[normal_dist<VaR])
ggplot()+
geom_density(aes(logret, geom ='density', col = 'returns'))+
geom_density(aes(normal_dist, col = 'normal'))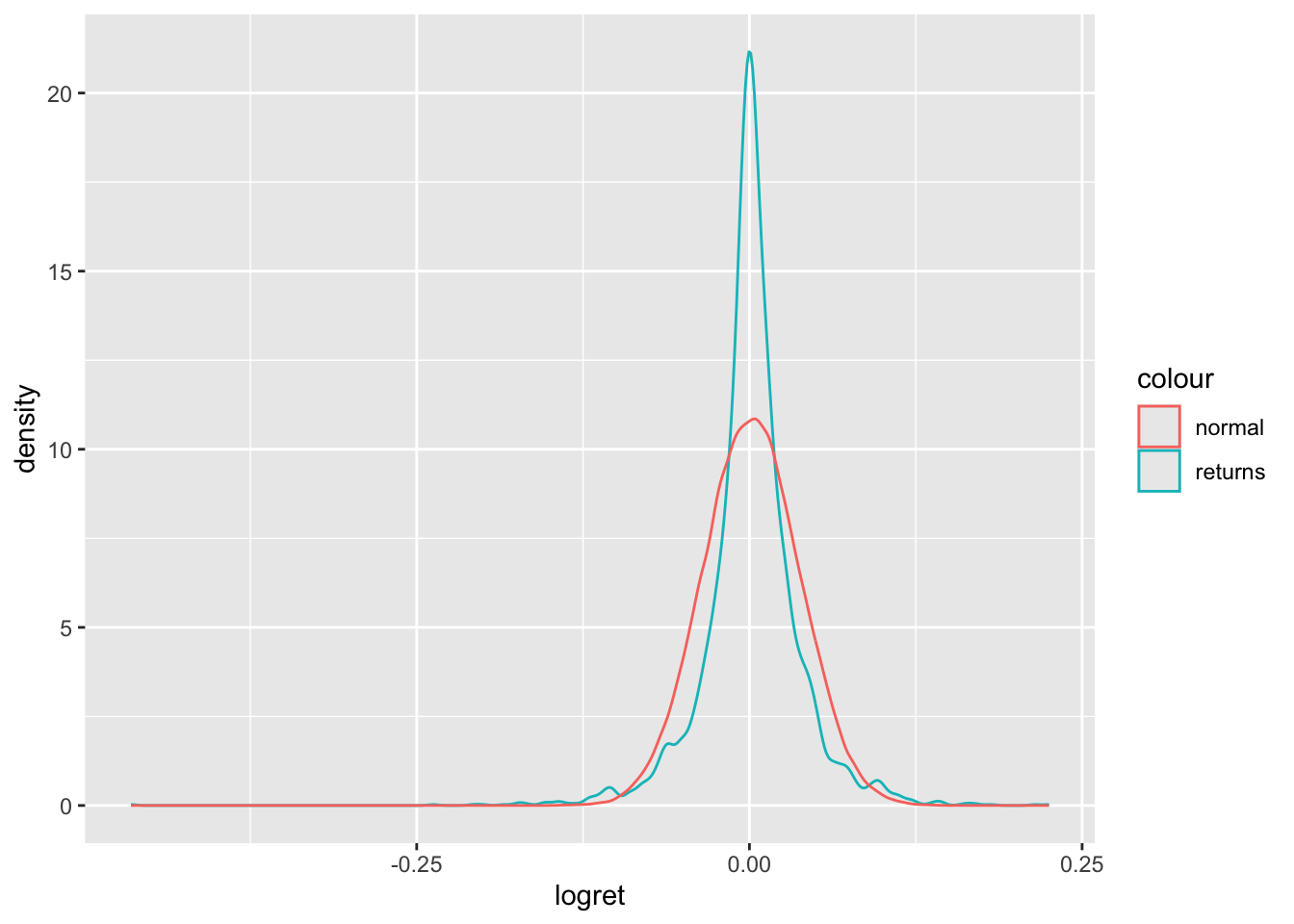
Figure 6.4: Densidad de rendimientos del Bitcoin Vs. una distribución normal
## [1] 14.4## [1] -0.726.2 Prueba de normalidad
\(H_o: K=S=0\)
jarque.test(vector_ret)##
## Jarque-Bera Normality Test
##
## data: vector_ret
## JB = 20834, p-value < 0.00000000000000022
## alternative hypothesis: greater6.3 Modelos ARCH y GARCH Univariados
Para plantear el modelo, supongamos–por simplicidad–que hemos construido y estimado un modelo AR(1). Es decir, asumamos que el proceso subyacente para la media condicional está dada por: \[\begin{equation} X_t = a_0 + a_1 X_{t-1} + U_t \end{equation}\]
Donde \(| a_1 |< 1\) para garantizar la convergencia del proceso en el largo plazo, en el cual: \[\begin{eqnarray*} \mathbb{E}[X_t] & = & \frac{a_0 }{1 - a_1} = \mu \\ Var[X_t] & = & \frac{\sigma^2}{1 - a_1^2} \end{eqnarray*}\]
Ahora, supongamos que este tipo de modelos pueden ser extendidos y generalizados a un modelo ARMA(p, q), que incluya otras variables exógenas. Denotemos a \(\mathbf{Z}_t\) como el conjunto que incluye los componentes AR, MA y variables exógenas que pueden explicar a \(X_t\) de forma que el proceso estará dado por: \[\begin{equation} X_t = \mathbf{Z}_t \boldsymbol{\beta} + U_t \end{equation}\]
Donde \(U_t\) es un proceso estacionario que representa el error asociado a un proceso ARMA(p, q) y donde siguen diendo válidos los supuestos: \[\begin{eqnarray*} \mathbb{E}[U_t] & = & 0 \\ Var[U_t^2] & = & \sigma^2 \end{eqnarray*}\]
No obstante, en este caso podemos suponer que existe autocorrelación en el término de error al cuadrado que puede ser capturada por un proceso similar a uno de medias móviles (MA) dado por: \[\begin{equation} U_t^2 = \gamma_0 + \gamma_1 U_{t-1}^2 + \gamma_2 U_{t-2}^2 + \ldots + \gamma_q U_{t-q}^2 + \nu_t \end{equation}\]
Donde \(\nu_t\) es un ruido blanco y \(U_{t-i} = X_{t-i} - \mathbf{Z}_{t-i} \boldsymbol{\beta}\), $i = 1, 2 ,$. Si bien los procesos son estacionarios por los supuestos antes enunciados, la varianza condicional estará dada por: \[\begin{eqnarray*} \sigma^2_{t | t-1} & = & Var[ U_t | \Omega_{t-1} ] \\ & = & \mathbb{E}[ U^2_t | \Omega_{t-1} ] \end{eqnarray*}\]
Donde \(\Omega_{t-1} = \{U_{t-1}, U_{t-2}, \ldots \}\) es el conjunto de toda la información pasada de \(U_t\) y observada hasta el momento \(t-1\), por lo que: \[\begin{equation*} U_t | \Omega_{t-1} \sim \mathbb{D}(0, \sigma^2_{t | t-1}) \end{equation*}\]
Así, de forma similar a un proceso MA(q) podemos decir que la varianza condicional tendrá efectos ARCH de orden \(q\) (ARCH(q)) cuando: \[\begin{equation} \sigma^2_{t | t-1} = \gamma_0 + \gamma_1 U_{t-1}^2 + \gamma_2 U_{t-2}^2 + \ldots + \gamma_q U_{t-q}^2 \tag{6.1} \end{equation}\]
Donde \(\mathbb{E}[\nu_t] = 0\) y \(\gamma_0\) y \(\gamma_i \geq 0\), para \(i = 1, 2, \ldots, q-1\) y \(\gamma_q > 0\). Estas condiciones son necesarias para garantizar que la varianza sea positiva. En general, la varianza condicional se expresa de la forma \(\sigma^2_{t | t-1}\), no obstante, para facilitar la notación, nos referiremos en cada caso a esta simplemente como \(\sigma^2_{t}\).
Podemos generalizar esta situación si asumimos a la varianza condicional como dependiente de los valores de la varianza rezagados, es decir, como si fuera un proceso AR de orden \(p\) para la varianza y juntándolo con la ecuación (6.1). Bollerslev (1986) y Taylor (1986) generalizaron el problema de heterocedasticidad condicional. El modelo se conoce como GARCH(p, q), el cual se especifica como: \[\begin{eqnarray} \sigma^2_t & = & \gamma_0 + \gamma_1 U_{t-1}^2 + \gamma_2 U_{t-2}^2 + \ldots + \gamma_q U_{t-q}^2 \\ \nonumber & & + \beta_1 \sigma^2_{t-1} + \beta_2 \sigma^2_{t-2} + \ldots + \beta_p \sigma^2_{t-p} \tag{6.2} \end{eqnarray}\]
Donde las condiciones de no negatividad son que \(\gamma_0 > 0\), \(\gamma_i \geq 0\), \(i = 1, 2, \ldots, q-1\), \(\beta_j \geq 0\), \(j = 1, 2, \ldots, p-1\), \(\gamma_q > 0\) y \(\beta_p > 0\). Además, otra condición de convergencia es que: \[\begin{equation*} \gamma_1 + \ldots + \gamma_q + \beta_1 + \ldots + \beta_p < 1 \end{equation*}\]
Usando el operador rezago \(L\) en la ecuación (6.2) podemos obtener: \[\begin{equation} \sigma^2_t = \gamma_0 + \alpha(L) U_t^2 + \beta(L) \sigma^2_t \tag{6.3} \end{equation}\]
De donde podemos establecer: \[\begin{equation} \sigma^2_t = \frac{\gamma_0}{1 - \beta(L)} + \frac{\alpha(L)}{1 - \beta(L)} U_t^2 \end{equation}\]
Por lo que la ecuación (6.2) del GARCH(p, q) representa un ARCH(\(\infty\)): \[\begin{equation} \sigma^2_t = \frac{a_0}{1 - b_1 - b_2 - \ldots - b_p} + \sum_{i = 1}^\infty U_{t-i}^2 \end{equation}\]
6.3.1 Ejemplo ARCH(1)
Hasta ahora, las distribuciones utilizadas para medir el Valor en Riesgo de un activo (Bitcoin, en este caso) asumen que no existe correlación serial en los retornos diarios del activo. Observemos un par de gráficas de la función de autocorrelación para corroborar este hecho–ver la Figura 6.5–.
acf(logret)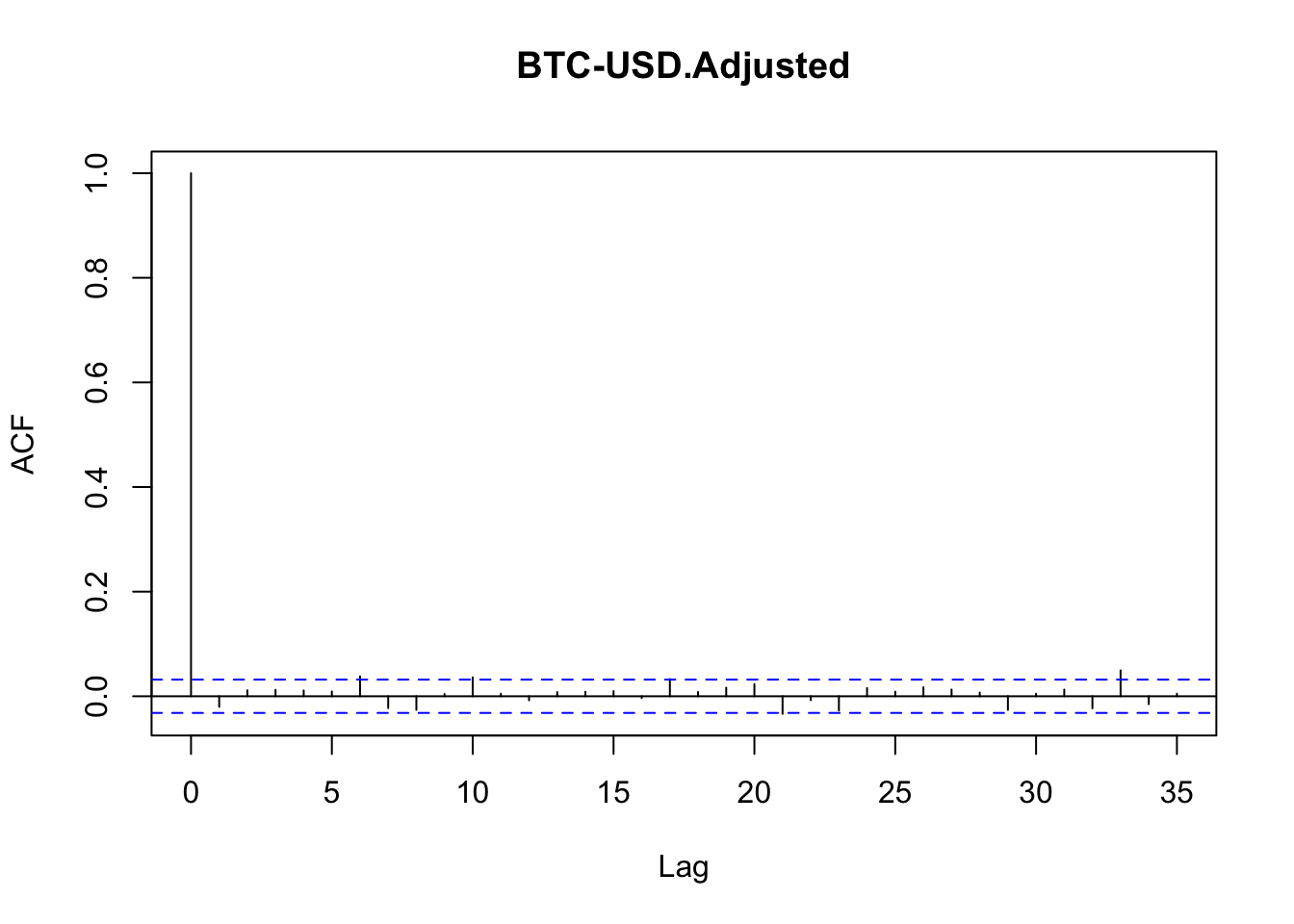
Figure 6.5: Función de autocorrelación parcial de lo rendimientos del Bitcoin
La idea de clusterización de volatilidad asume que períodos de alta volatilidad serán seguidos por alta volatilidad y viceversa. Por esta razón, la función de autocorrelación útil para saber si existen clústers de volatilidad es utilizando el valor absoluto, ya que lo que importa es saber si la serie está autocorrelacionada en la magnitud de los movimientos. La Figura 6.6 muestra el comportamiento de los rendimientos en valor absoluto y la Figura 6.7 la función de autocorrelación parcial.
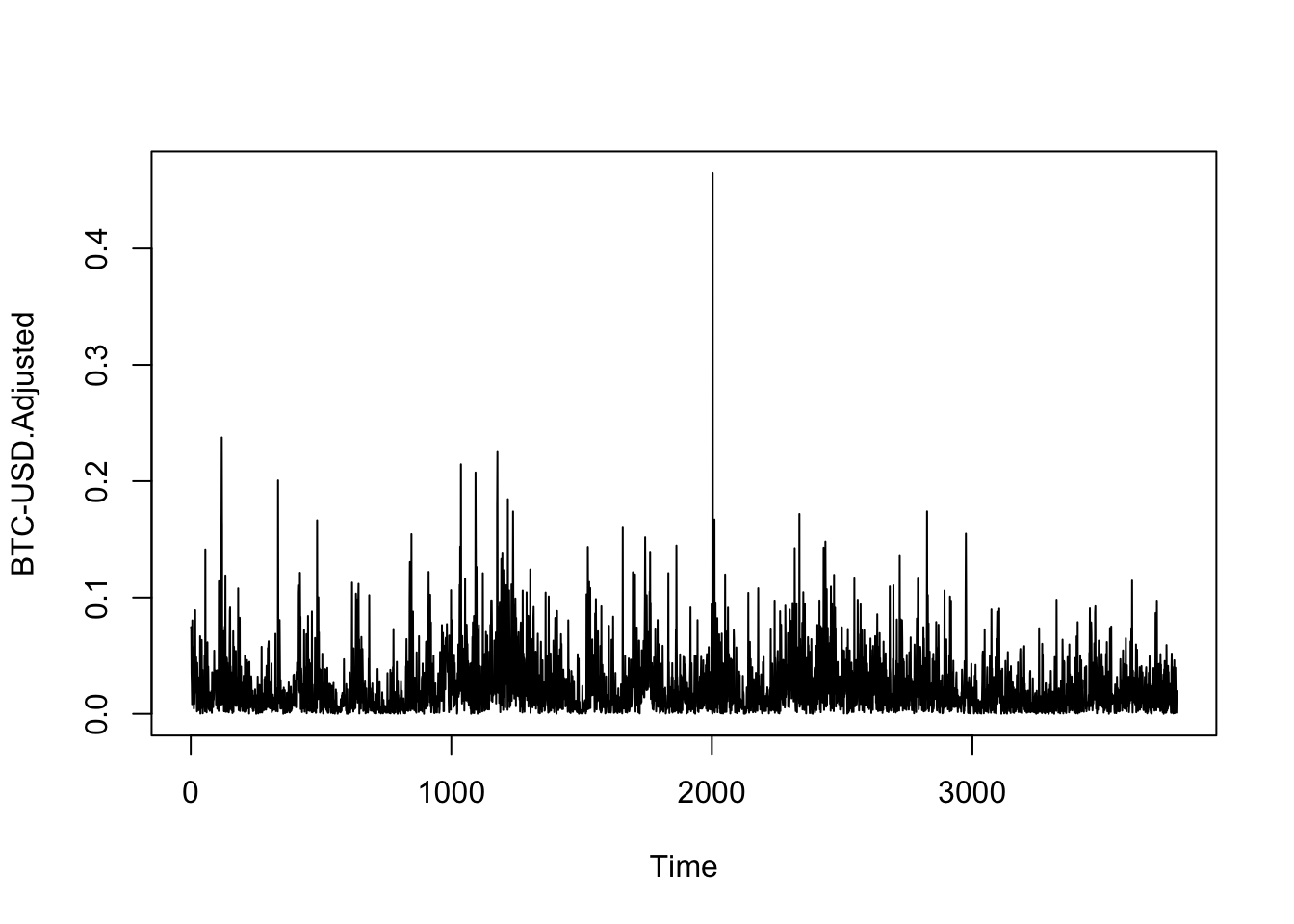
Figure 6.6: Evolución de los rendimientos del Bitcoin en valor absoluto
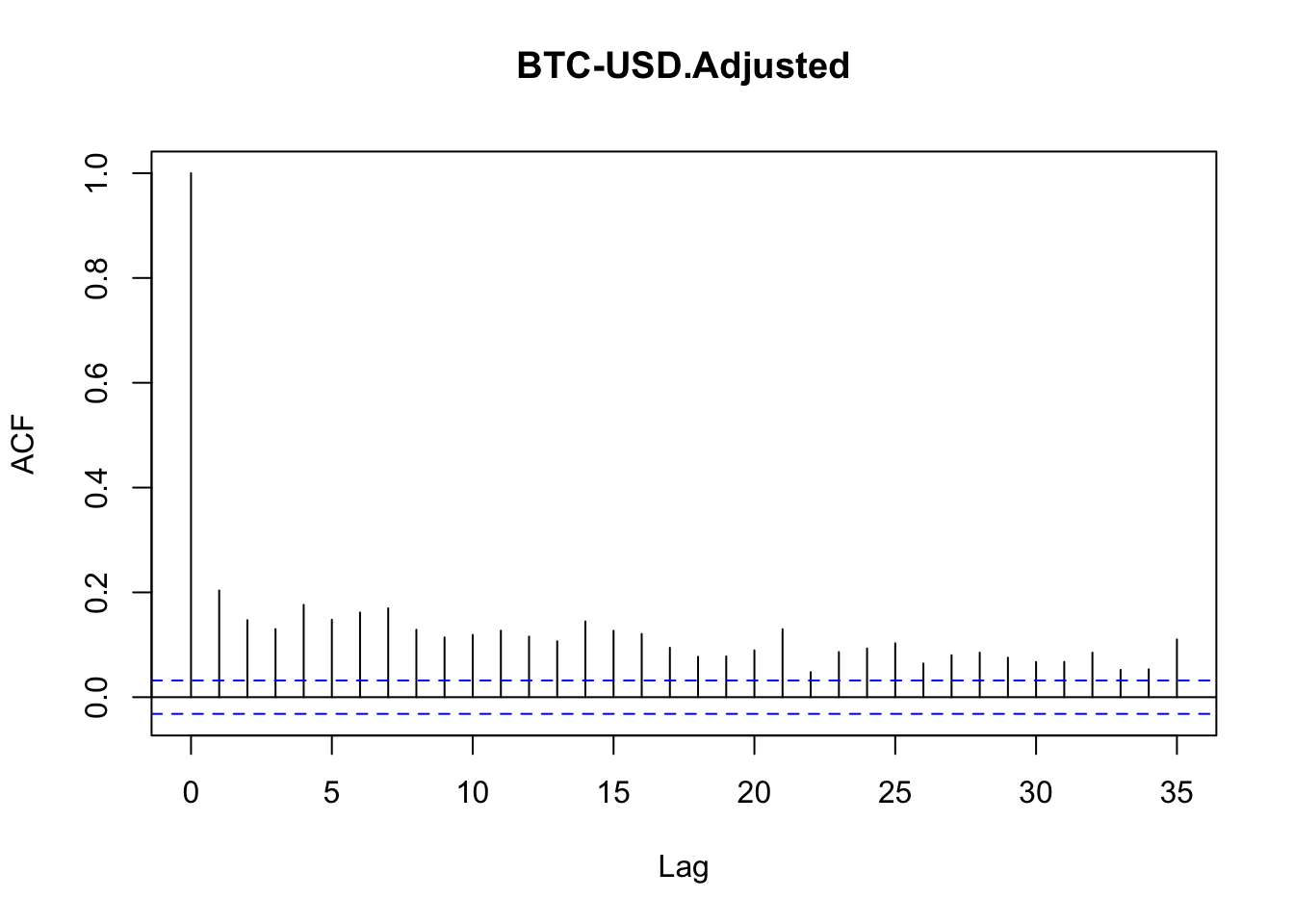
Figure 6.7: Función de autocorrelación parcial de los rendimientos del Bitcoin en valor absoluto
Otra manera de corroborar esta idea es volviendo IID nuestra serie de datos y observar que de este modo se pierde la autocorrelación serial, lo que refuerza la idea de que en esta serie existen clusters de volatilidad.
logret_random <- sample(as.vector(logret), size = length(logret), replace = FALSE)
acf(abs(logret_random))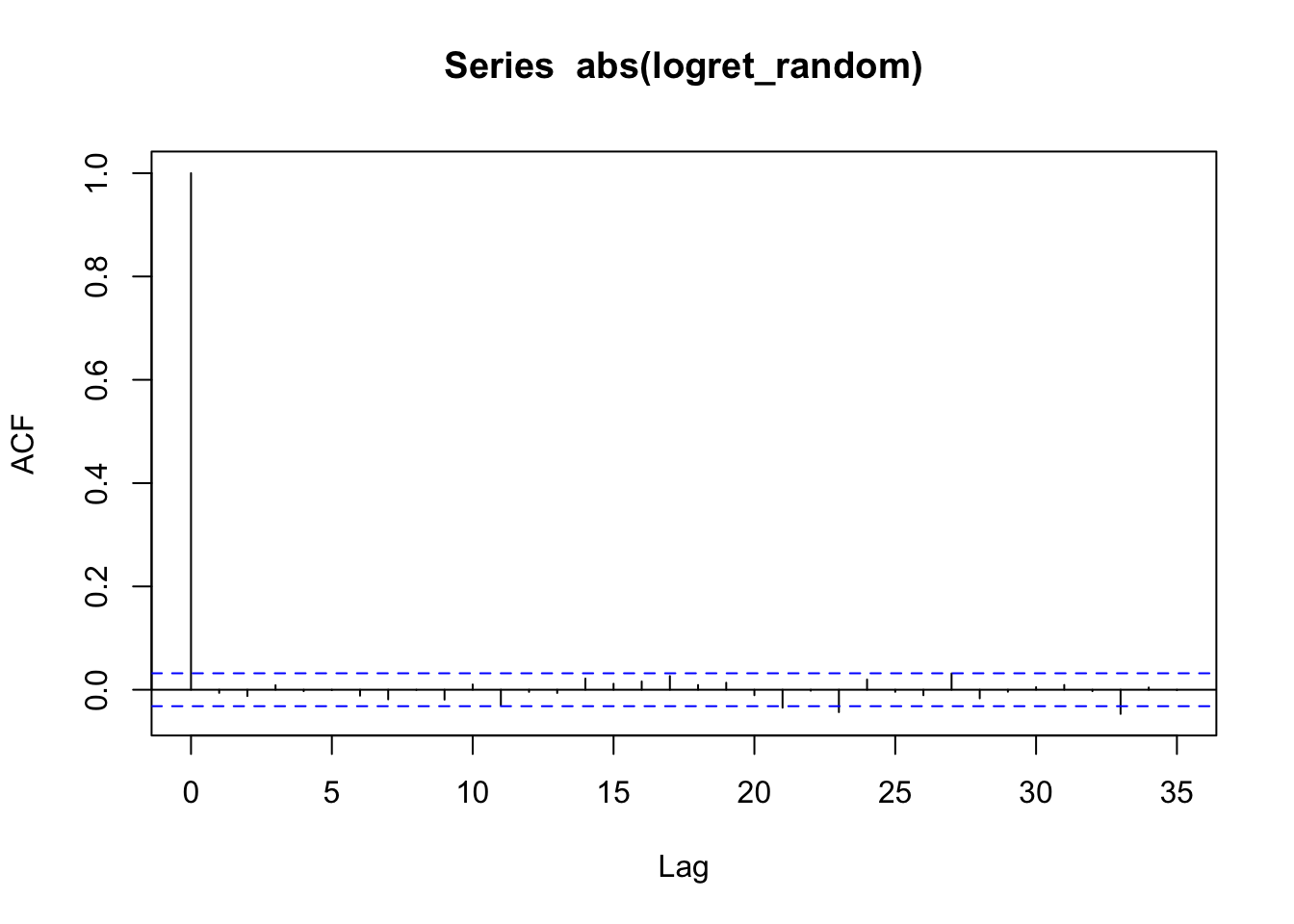
Figure 6.8: Función de autocorrelación parcial de los rendimientos del Bitcoin en valor absoluto
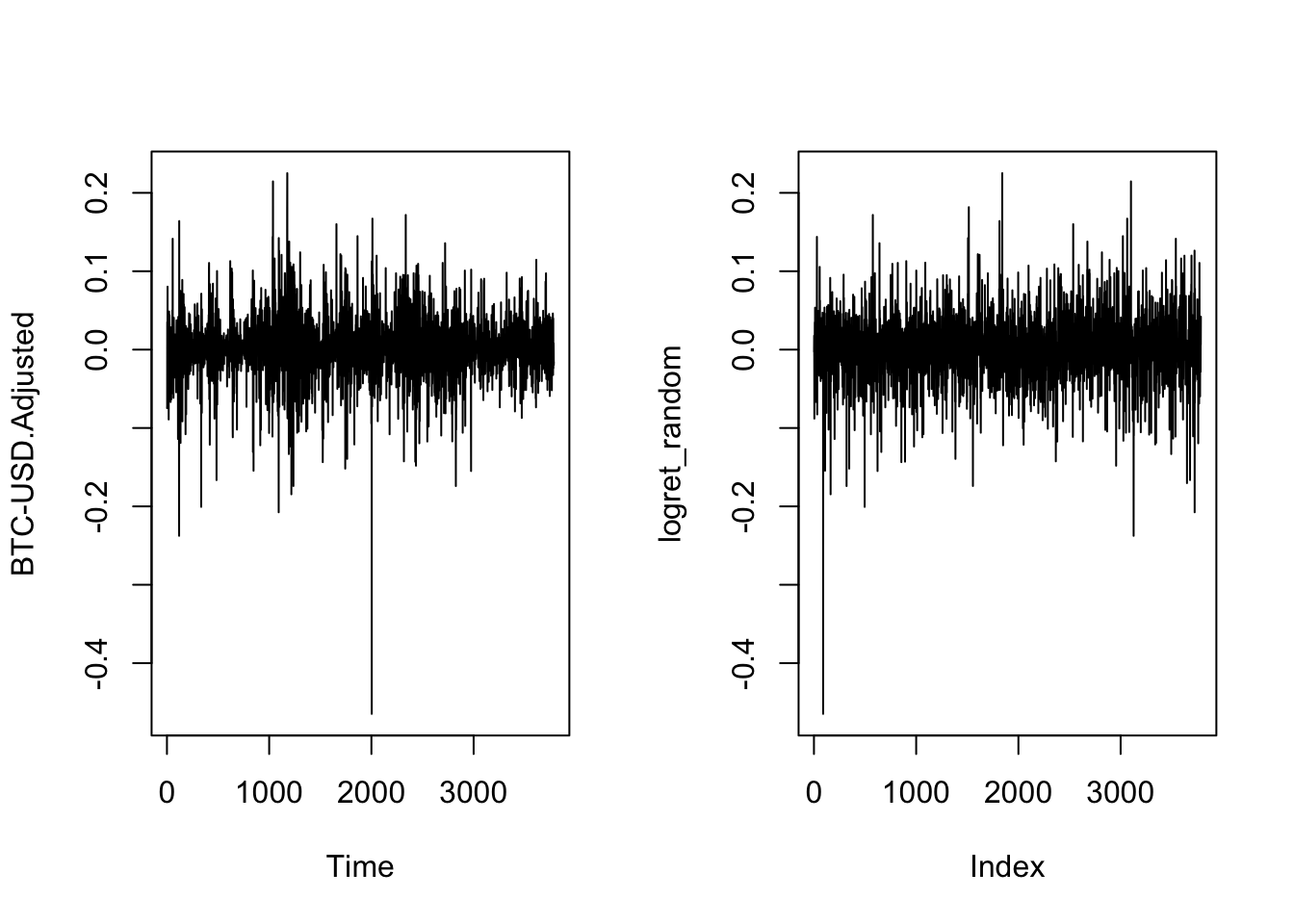
Figure 6.9: Función de autocorrelación parcial de los rendimientos del Bitcoin en valor absoluto
Ahora busquemos una prueba formal. El primer enfoque para comprobar aceptar o rechazar la hipótesis de que necesitamos estimar un ARCH(q) es realizar una prueba de efectos ARCH. De acuerdo con esta, nuestros datos de Bitcoin muestran que se rechaza la hipótesis de no efectos ARCH. Esta prueba resulta del siguiente código de R:
##
## Time series regression with "ts" data:
## Start = 1, End = 3785
##
## Call:
## dynlm(formula = logret ~ 1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.46616 -0.01409 -0.00011 0.01542 0.22369
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0014262 0.0005913 2.412 0.0159 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.03638 on 3784 degrees of freedom##
## Time series regression with "ts" data:
## Start = 2, End = 3785
##
## Call:
## dynlm(formula = ehatsq ~ L(ehatsq))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.016924 -0.001151 -0.001019 -0.000314 0.216151
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.00115055 0.00008097 14.210 < 0.0000000000000002 ***
## L(ehatsq) 0.12955356 0.01612192 8.036 0.00000000000000123 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.004805 on 3782 degrees of freedom
## Multiple R-squared: 0.01679, Adjusted R-squared: 0.01653
## F-statistic: 64.58 on 1 and 3782 DF, p-value: 0.000000000000001231
acf(ARCH_m$residuals)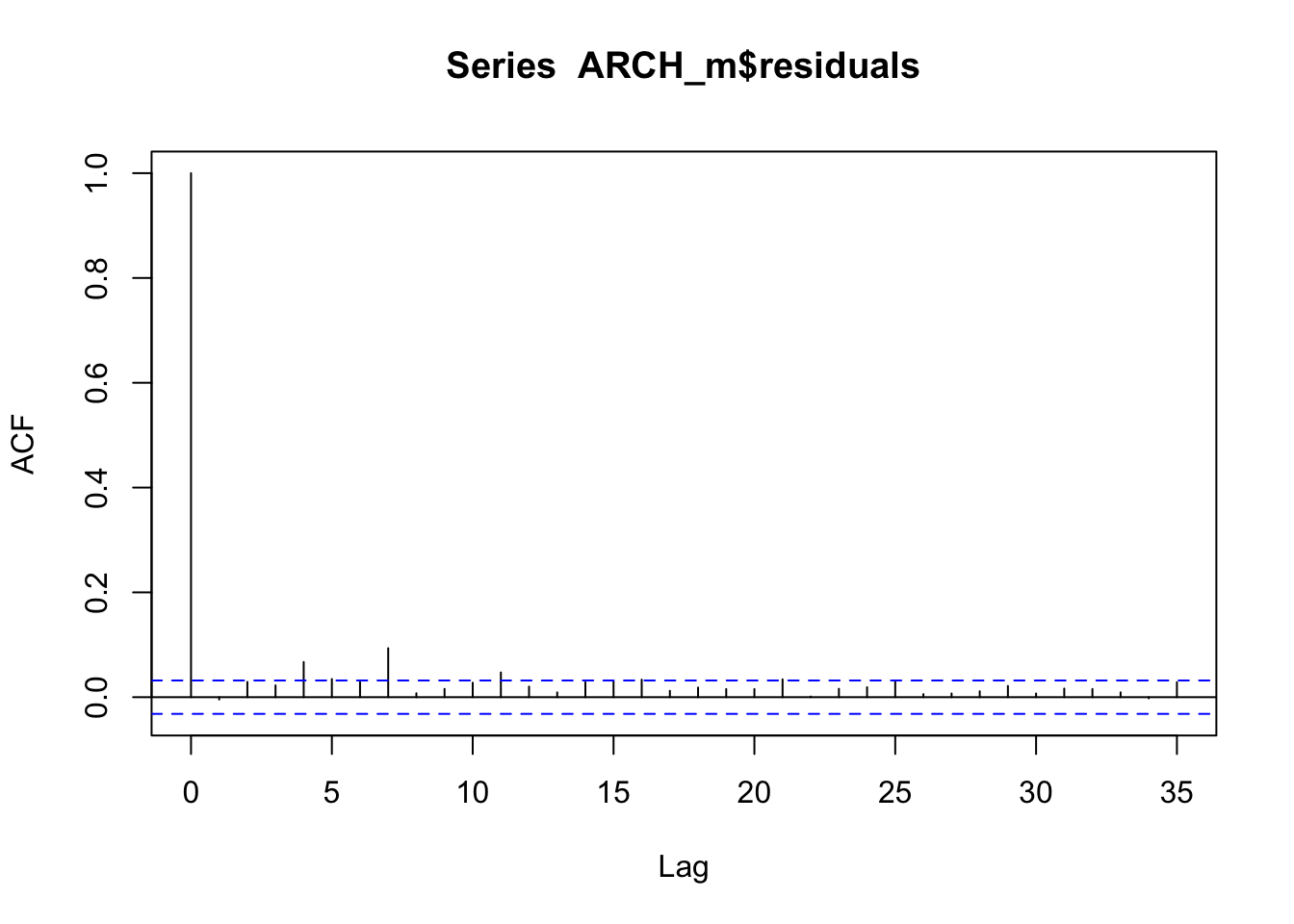
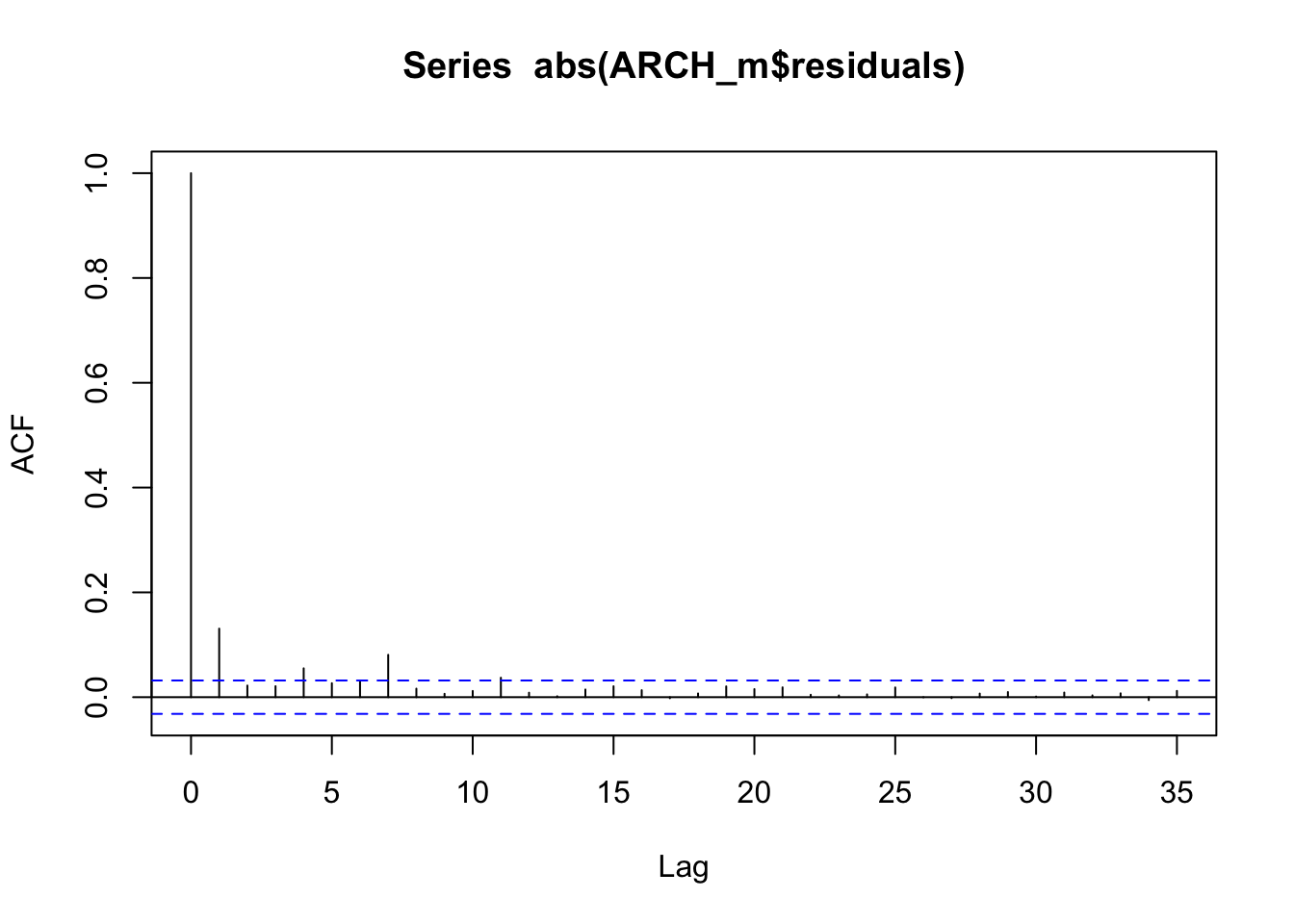
ArchTest(logret, lags = 1, demean = TRUE)##
## ARCH LM-test; Null hypothesis: no ARCH effects
##
## data: logret
## Chi-squared = 63.525, df = 1, p-value = 0.000000000000001584La prueba puede repetirse para diferentes especificaciones de ARCH, sin embargo, para efectos ilustrativos usaremos un ARCH(1). Estimemos un ARCH(1), considerando la siguente especificación:
\[\begin{eqnarray*} Y_t & = & \mu+\sqrt{h_t}\varepsilon_t \\ h_t & = & \omega+\alpha_ih_{t-i}+u_t \\ \varepsilon & \sim & N(0,1) \end{eqnarray*}\]
Considerando que la media es una AR(2), los resultados de esta estimación son los siguientes:
| Parameter | Estimate | Std. Error | t value | Pr(\(>\mid t\mid\)) |
|---|---|---|---|---|
| mu | 0.001642394 | 0.0003553101 | 4.622424 | 3.792818e-06 |
| ar1 | -0.051859993 | 0.0160262284 | -3.235945 | 1.212408e-03 |
| ar2 | -0.001225748 | 0.0132050756 | -0.092824 | 9.260434e-01 |
| omega | 0.001956396 | 0.0004839458 | 4.042593 | 5.286335e-05 |
| alpha1 | 0.730450078 | 0.2140120509 | 3.413126 | 6.422226e-04 |
| shape | 2.347586356 | 0.1135148037 | 20.680883 | 0.000000e+00 |
Notas:
-
Primera línea en negrita como título de la tabla (Markdown no tiene un
\caption{}como LaTeX).
- Bajo el título, se añade un párrafo en itálicas con los valores adicionales (\(\sigma^2\), log-likelihood, AIC, etc.).
- La fila de encabezados va seguida por una fila de separadores (
|:---|---:|etc.) para indicar la alineación a la izquierda, derecha o centro.
- Las celdas con datos numéricos se alinean a la derecha (
:---:o---:) para mantener la estética de los números.
- Si prefieres, puedes omitir la columna de “Notas” y añadir la información directamente en el título de la tabla o en un párrafo posterior.
library(rugarch)
auto.arima(logret)## Series: logret
## ARIMA(2,0,0) with non-zero mean
##
## Coefficients:
## ar1 ar2 mean
## -0.0200 0.0110 0.0014
## s.e. 0.0163 0.0163 0.0006
##
## sigma^2 = 0.001324: log likelihood = 7173.27
## AIC=-14338.54 AICc=-14338.53 BIC=-14313.59
#?ugarchspec
model.spec = ugarchspec( variance.model = list(model = 'sGARCH' ,
garchOrder = c(1, 0)),
mean.model = list(armaOrder = c(2,0)),
distribution.model = "std")
#?ugarchfit
arch.fit = ugarchfit(spec = model.spec , data = logret,
solver = 'solnp')
arch.fit@fit$matcoef## Estimate Std. Error t value Pr(>|t|)
## mu 0.001634199 0.0003554176 4.59796875 0.00000426630
## ar1 -0.051571141 0.0160278553 -3.21759461 0.00129270384
## ar2 -0.001173354 0.0132063519 -0.08884774 0.92920291820
## omega 0.001956746 0.0004877426 4.01184036 0.00006024724
## alpha1 0.730831252 0.2153966887 3.39295491 0.00069143019
## shape 2.347546285 0.1143766754 20.52469420 0.00000000000
boot.garch <- ugarchboot(arch.fit,
method = "Partial",
sampling = "raw", #bootstrap from fitted varepsilon
n.ahead = 1, #simulation horizon
n.bootpred = 100000, #number of simulations
solver = "solnp")
boot.garch##
## *-----------------------------------*
## * GARCH Bootstrap Forecast *
## *-----------------------------------*
## Model : sGARCH
## n.ahead : 1
## Bootstrap method: partial
## Date (T[0]): 3785-01-01
##
## Series (summary):
## min q.25 mean q.75 max forecast[analytic]
## t+1 -0.49272 -0.011029 0.002131 0.016278 0.21349 0.002559
## .....................
##
## Sigma (summary):
## min q0.25 mean q0.75 max forecast[analytic]
## t+1 0.046993 0.046993 0.046993 0.046993 0.046993 0.046993
## .....................6.4 Ejemplo GARCH(0,1)
Estimemos un GARCH(0,1) usando la siguiente especificación: \[\begin{eqnarray*} Y_t & = & \mu+\sqrt{h_t}\varepsilon_t \\ h_t & = & \omega+\beta_i \sigma^2_{t-i}+u_t \\ \varepsilon & \sim & N(0,1) \end{eqnarray*}\]
Considerando que la media es una AR(2), los resultados de esta estimación son los siguientes:
| Parameter | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| mu | 1.743510e-03 | 3.728562e-04 | 4.6760931 | 2.923919e-06 |
| ar1 | -6.104183e-02 | 1.366530e-02 | -4.4669219 | 7.935308e-06 |
| ar2 | -4.231427e-03 | 1.311300e-02 | -0.3226895 | 7.469304e-01 |
| omega | 3.843436e-06 | 6.414905e-08 | 59.9141495 | 0.000000e+00 |
| beta1 | 9.981016e-01 | 3.215075e-05 | 31044.4303 | 0.000000e+00 |
| shape | 2.515980e+00 | 2.796609e-02 | 89.9653552 | 0.000000e+00 |
model.spec = ugarchspec(variance.model = list(model = 'sGARCH' ,
garchOrder = c(0,1)),
mean.model = list(armaOrder = c(2,0)),
distribution.model = "std")
fit.garch.n = ugarchfit(spec = model.spec, data = logret,
solver = "solnp")
fit.garch.n@fit$matcoef## Estimate Std. Error t value Pr(>|t|)
## mu 0.001732549251 0.00037335216769 4.6405228 0.000003475288
## ar1 -0.060564251420 0.01366669410752 -4.4315217 0.000009357040
## ar2 -0.003165659273 0.01312052794226 -0.2412753 0.809341755744
## omega 0.000004030097 0.00000006466761 62.3201687 0.000000000000
## beta1 0.998010983096 0.00003420421161 29178.0145209 0.000000000000
## shape 2.514422127328 0.02778984749145 90.4798822 0.000000000000
boot.garch <- ugarchboot(fit.garch.n,
method = "Partial",
sampling = "raw", #bootstrap from fitted varepsilon
n.ahead = 1, #simulation horizon
n.bootpred = 100000, #number of simulations
solver = "solnp")
boot.garch##
## *-----------------------------------*
## * GARCH Bootstrap Forecast *
## *-----------------------------------*
## Model : sGARCH
## n.ahead : 1
## Bootstrap method: partial
## Date (T[0]): 3785-01-01
##
## Series (summary):
## min q.25 mean q.75 max forecast[analytic]
## t+1 -0.46517 -0.012305 0.002125 0.017968 0.2412 0.002863
## .....................
##
## Sigma (summary):
## min q0.25 mean q0.75 max forecast[analytic]
## t+1 0.045009 0.045009 0.045009 0.045009 0.045009 0.045009
## .....................6.4.1 Selección GARCH(p,q) óptimo
¿Cómo seleccionamos el órden adecuado para un GARCH(p,q)? Acá una respuesta.
\(Y_t = \mu+\sqrt{h_t}\varepsilon_t\)
\(h_t = \omega+\beta_ih_{t-i}+\alpha_i\varepsilon^2_{t-i}+u_t\)
\(\varepsilon \sim N(0,1)\)
6.4.1.1 Criterios de información
| Criterio | Valor |
|---|---|
| Akaike | -4.083927 |
| Bayes | -4.074035 |
| Shibata | -4.083932 |
| Hannan-Quinn | -4.080410 |
infocriteria(fit.garch.n)##
## Akaike -4.084107
## Bayes -4.074217
## Shibata -4.084112
## Hannan-Quinn -4.0805916.4.1.2 Selección del modelo óptimo
Podemos hacer una búsqueda del mejor modelo de entre varios que probemos en un espectro de hasta un GARCH(4,4). Los resultados son los reportados en el siguiente Cuadro.
| q | p | AIC | Óptimo |
|---|---|---|---|
| 1 | 1 | -10.93647 | 0 |
| 1 | 2 | -10.93657 | 0 |
| 1 | 3 | -10.93799 | 0 |
| 1 | 4 | -10.93727 | 0 |
| 2 | 1 | -10.93579 | 0 |
| 2 | 2 | -10.93607 | 0 |
| 2 | 3 | -10.93743 | 0 |
| 2 | 4 | -10.93510 | 0 |
| 3 | 1 | -10.93524 | 0 |
| 3 | 2 | -10.93510 | 0 |
| 3 | 3 | -10.93765 | 0 |
| 3 | 4 | -10.93645 | 0 |
| 4 | 1 | -10.93840 | 0 |
| 4 | 2 | -10.93935 | 1 |
| 4 | 3 | -10.93924 | 0 |
| 4 | 4 | -10.93816 | 0 |
source("Lag_Opt_GARCH.R")
Lag_Opt_GARCH(ehatsq,4,4)## q p AIC Optimo
## [1,] 1 1 -10.93717 0
## [2,] 1 2 -10.93691 0
## [3,] 1 3 -10.93883 0
## [4,] 1 4 -10.93810 0
## [5,] 2 1 -10.93664 0
## [6,] 2 2 -10.93672 0
## [7,] 2 3 -10.93641 0
## [8,] 2 4 -10.93591 0
## [9,] 3 1 -10.93617 0
## [10,] 3 2 -10.93594 0
## [11,] 3 3 -10.93849 0
## [12,] 3 4 -10.93729 0
## [13,] 4 1 -10.93924 0
## [14,] 4 2 -10.94022 1
## [15,] 4 3 -10.93976 0
## [16,] 4 4 -10.93942 06.4.1.3 Estimación de modelo óptimo
De esta forma, el modelo óptimo es un GARCH(2,4). Los resultados de la estimación son los del Cuadro
| Parameter | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| mu | 1.353612e-03 | 3.233488e-04 | 4.186229e+00 | 2.836277e-05 |
| ar1 | -4.916331e-02 | 1.495855e-02 | -3.286636e+00 | 1.013919e-03 |
| ar2 | 7.273432e-04 | 1.385161e-02 | 5.250964e-02 | 9.581226e-01 |
| omega | 2.759072e-05 | 5.151381e-06 | 5.355984e+00 | 8.509188e-08 |
| alpha1 | 1.290996e-01 | 2.165606e-02 | 5.961363e+00 | 2.501419e-09 |
| alpha2 | 1.768468e-07 | 3.676320e-02 | 4.810430e-06 | 9.999962e-01 |
| alpha3 | 6.424436e-08 | 2.663630e-02 | 2.411910e-06 | 9.999981e-01 |
| alpha4 | 3.333343e-02 | 2.238762e-02 | 1.488923e+00 | 1.365077e-01 |
| beta1 | 4.260058e-01 | 2.263614e-01 | 1.881972e+00 | 5.983983e-02 |
| beta2 | 4.105609e-01 | 1.819274e-01 | 2.256730e+00 | 2.402498e-02 |
| shape | 3.183045e+00 | 1.305307e-01 | 2.438541e+01 | 0.000000e+00 |
model.spec = ugarchspec(variance.model = list(model = 'sGARCH',
garchOrder = c(4,2)),
mean.model = list(armaOrder = c(2,0)),
distribution.model = "std")
model.fit = ugarchfit(spec = model.spec , data = logret,
solver = 'solnp')
model.fit@fit$matcoef## Estimate Std. Error t value Pr(>|t|)
## mu 0.0013463448938 0.000323450602 4.16244361401 0.000031485990629
## ar1 -0.0488340334201 0.014958604103 -3.26461166323 0.001096142473348
## ar2 0.0007806639661 0.013852428181 0.05635574903 0.955058408055019
## omega 0.0000275911232 0.000005169389 5.33740503074 0.000000094286259
## alpha1 0.1291123913696 0.021657036600 5.96168320494 0.000000002496528
## alpha2 0.0000001167147 0.036821188483 0.00000316977 0.999997470889172
## alpha3 0.0000000357534 0.026602826782 0.00000134397 0.999998927667146
## alpha4 0.0334049097266 0.022389819504 1.49196869230 0.135707352966684
## beta1 0.4258402873418 0.226518488970 1.87993611152 0.060116785623216
## beta2 0.4106422585493 0.182128432146 2.25468507970 0.024153102839025
## shape 3.1840994007682 0.130709861275 24.36005493171 0.000000000000000
boot.garch <- ugarchboot(model.fit,
method = "Partial",
sampling = "raw", #bootstrap from fitted varepsilon
n.ahead = 1, #simulation horizon
n.bootpred = 100000, #number of simulations
solver = "solnp")
boot.garch##
## *-----------------------------------*
## * GARCH Bootstrap Forecast *
## *-----------------------------------*
## Model : sGARCH
## n.ahead : 1
## Bootstrap method: partial
## Date (T[0]): 3785-01-01
##
## Series (summary):
## min q.25 mean q.75 max forecast[analytic]
## t+1 -0.30584 -0.008737 0.002116 0.013685 0.23587 0.002168
## .....................
##
## Sigma (summary):
## min q0.25 mean q0.75 max forecast[analytic]
## t+1 0.025129 0.025129 0.025129 0.025129 0.025129 0.025129
## .....................6.4.1.4 Forecasting with GARCH(1,1)
Para realizar pronósticos con la estimación de un GARCH, utilizando la librería rugarch, es necesario utilizar la función ugarchforecast().
model.spec = ugarchspec(variance.model = list(model = 'sGARCH',
garchOrder = c(1,1)),
mean.model = list(armaOrder = c(4,2)),
distribution.model = "std")
model.fit = ugarchfit(spec = model.spec , data = logret,
solver = 'solnp')
spec = getspec(model.fit)
setfixed(spec) <- as.list(coef(model.fit))Esta función precisa como argumentos nuestra estimación del modelo GARCH, con una modificación en la manera en que se presentan los coeficientes, realizada en la última línea del código anterior y que llamamos spec. n.ahead es el número de periodos que vamos a pronosticar, n.roll señala el número de pronósticos móviles que utilizaremos, en caso de que haya más información para realizar el pronóstico. Finalmente damos como input nuestro set de datos y como producto obtendremos el pronostico de Sigma tanto como de la serie.
forecast = ugarchforecast(spec, n.ahead = 12, n.roll = 0, logret)
sigma(forecast)## 3785-01-01
## T+1 0.02537095
## T+2 0.02571801
## T+3 0.02606010
## T+4 0.02639743
## T+5 0.02673017
## T+6 0.02705849
## T+7 0.02738256
## T+8 0.02770251
## T+9 0.02801850
## T+10 0.02833065
## T+11 0.02863909
## T+12 0.02894394
fitted(forecast)## 3785-01-01
## T+1 0.003014905
## T+2 0.002208362
## T+3 0.001815263
## T+4 0.002000821
## T+5 0.001847454
## T+6 0.001985169
## T+7 0.001851648
## T+8 0.001969917
## T+9 0.001854931
## T+10 0.001956140
## T+11 0.001857074
## T+12 0.001943646
forecast##
## *------------------------------------*
## * GARCH Model Forecast *
## *------------------------------------*
## Model: sGARCH
## Horizon: 12
## Roll Steps: 0
## Out of Sample: 0
##
## 0-roll forecast [T0=]:
## Series Sigma
## T+1 0.003015 0.02537
## T+2 0.002208 0.02572
## T+3 0.001815 0.02606
## T+4 0.002001 0.02640
## T+5 0.001847 0.02673
## T+6 0.001985 0.02706
## T+7 0.001852 0.02738
## T+8 0.001970 0.02770
## T+9 0.001855 0.02802
## T+10 0.001956 0.02833
## T+11 0.001857 0.02864
## T+12 0.001944 0.028946.5 Modelos ARCH y GARCH Multivariados
De forma similar a los modelos univariados, los modelos multivariados de heterocedasticidad condicional asumen una estructura de la media condicional. En este caso, descrita por un VAR(p) cuyo proceso estocástico \(\mathbf{X}\) es estacionario de dimensión \(k\). De esta forma, la expresión reducida del modelo o el proceso VAR(p) estará dado por: \[\begin{equation} \mathbf{X}_t = \boldsymbol{\delta} + \mathbf{A_1} \mathbf{X}_{t-1} + \mathbf{A_2} \mathbf{X}_{t-2} + \ldots + \mathbf{A_p} \mathbf{X}_{t-p} + \mathbf{U}_{t} \end{equation}\]
Donde cada uno de las \(\mathbf{A_i}\), \(i = 1, 2, \ldots, p\), son matrices cuadradas de dimensión \(k\) y \(\mathbf{U}_t\) representa un vector de dimensión \(k \times 1\) con los residuales en el momento del tiempo \(t\) que son un proceso puramente aleatorio. También se incorpora un vector de términos constantes denominado como \(\boldsymbol{\delta}\), el cual es de dimensión \(k \times 1\) –en este caso también es posible incorporar procesos determinísticos adicionales–.
Así, suponemos que el término de error tendrá estructura de vector: \[\begin{equation*} \mathbf{U}_t = \begin{bmatrix} U_{1t} \\ U_{2t} \\ \vdots \\ U_{Kt} \end{bmatrix} \end{equation*}\]
De forma que diremos que: \[\begin{equation*} \mathbf{U}_t | \Omega_{t-1} \sim (0, \Sigma_{t | t-1}) \end{equation*}\]
Dicho lo anterior, entonces, el modelo ARCH(q) multivariado será descrito por: \[\begin{equation} Vech(\Sigma_{t | t-1}) = \boldsymbol{\gamma}_0 + \Gamma_1 Vech(\mathbf{U}_{t-1} \mathbf{U}_{t-1}') + \ldots + \Gamma_q Vech(\mathbf{U}_{t-q} \mathbf{U}_{t-q}') (\#eq:M_ARCH) \end{equation}\]
Donde \(Vech\) es un operador que apila en un vector la parte superior de la matriz a la cual se le aplique, \(\boldsymbol{\gamma}_0\) es un vector de constantes, \(\Gamma_i\), \(i = 1, 2, \ldots\) son matrices de coeficientes asociados a la estimación.
Para ilustrar la ecuación @ref(eq:M_ARCH), tomemos un ejemplo de \(K = 2\), de esta forma tenemos que un M-ARCH(1) será: \[\begin{equation*} \Sigma_{t | t-1} = \begin{bmatrix} \sigma^2_{1, t | t-1} & \sigma_{12, t | t-1} \\ \sigma_{21, t | t-1} & \sigma^2_{2, t | t-1} \end{bmatrix} = \begin{bmatrix} \sigma_{11, t} & \sigma_{12, t} \\ \sigma_{21, t} & \sigma_{22, t} \end{bmatrix} = \Sigma_{t} \end{equation*}\]
Donde hemos simplificado la notación de las varianzas y la condición de que están en función de \(t-1\). Así, \[\begin{equation*} Vech(\Sigma_{t}) = Vech \begin{bmatrix} \sigma_{11, t} & \sigma_{12, t} \\ \sigma_{21, t} & \sigma_{22, t} \end{bmatrix} = \begin{bmatrix} \sigma_{11, t} \\ \sigma_{12, t} \\ \sigma_{22, t} \end{bmatrix} \end{equation*}\]
De esta forma, podemos establecer el modelo M-ARCH(1) con \(K = 2\) será de la forma: \[\begin{equation*} \begin{bmatrix} \sigma_{11, t} \\ \sigma_{12, t} \\ \sigma_{22, t} \end{bmatrix} = \begin{bmatrix} \gamma_{10} \\ \gamma_{20} \\ \gamma_{30} \end{bmatrix} + \begin{bmatrix} \gamma_{11} & \gamma_{12} & \gamma_{13} \\ \gamma_{21} & \gamma_{22} & \gamma_{23} \\ \gamma_{31} & \gamma_{32} & \gamma_{33} \end{bmatrix} \begin{bmatrix} U^2_{1, t-1} \\ U_{1, t-1} U_{2, t-1} \\ U^2_{2, t-1} \end{bmatrix} \end{equation*}\]
Como notarán, este tipo de procedimientos implica la estimación de muchos parámetros. En esta circunstancia, se suelen estimar modelos restringidos para reducir el número de coeficientes estimados. Por ejemplo, podríamos querer estimar un caso como: \[\begin{equation*} \begin{bmatrix} \sigma_{11, t} \\ \sigma_{12, t} \\ \sigma_{22, t} \end{bmatrix} = \begin{bmatrix} \gamma_{10} \\ \gamma_{20} \\ \gamma_{30} \end{bmatrix} + \begin{bmatrix} \gamma_{11} & 0 & 0 \\ 0 & \gamma_{22} & 0 \\ 0 & 0 & \gamma_{33} \end{bmatrix} \begin{bmatrix} U^2_{1, t-1} \\ U_{1, t-1} U_{2, t-1} \\ U^2_{2, t-1} \end{bmatrix} \end{equation*}\]
Finalmente y de forma análoga al caso univariado, podemos plantear un modelo M-GARCH(p, q) como: \[\begin{equation} Vech(\Sigma_{t | t-1}) = \boldsymbol{\gamma}_0 + \sum_{j = 1}^q \Gamma_j Vech(\mathbf{U}_{t-j} \mathbf{U}_{t-j}') + \sum_{m = 1}^p \mathbf{G}_m Vech(\Sigma_{t-m | t-m-1}) \label{M_GARCH} \end{equation}\]
Donde cada una de las \(\mathbf{G}_m\) es una matriz de coeficientes. Para ilustrar este caso, retomemos el ejemplo anterior, pero ahora para un modelo M-GARCH(1, 1) con \(K = 2\) de forma que tendríamos: \[\begin{eqnarray*} \begin{bmatrix} \sigma_{11, t} \\ \sigma_{12, t} \\ \sigma_{22, t} \end{bmatrix} & = & \begin{bmatrix} \gamma_{10} \\ \gamma_{20} \\ \gamma_{30} \end{bmatrix} + \begin{bmatrix} \gamma_{11} & \gamma_{12} & \gamma_{13} \\ \gamma_{21} & \gamma_{22} & \gamma_{23} \\ \gamma_{31} & \gamma_{32} & \gamma_{33} \end{bmatrix} \begin{bmatrix} U^2_{1, t-1} \\ U_{1, t-1} U_{2, t-1} \\ U^2_{2, t-1} \end{bmatrix} \\ & & + \begin{bmatrix} g_{11} & g_{12} & g_{13} \\ g_{21} & g_{22} & g_{23} \\ g_{31} & g_{32} & g_{33} \end{bmatrix} \begin{bmatrix} \sigma_{11, t-1} \\ \sigma_{12, t-1} \\ \sigma_{22, t-1} \end{bmatrix} \end{eqnarray*}\]
6.6 Pruebas para detectar efectos ARCH
La prueba que mostraremos es conocida como una ARCH-LM, la cual está basada en una regresión de los residuales estimados de un modelo VAR(p) o cualquier otra estimación que deseemos probar, con el objeto de determinar si existen efectos ARCH –esta prueba se puede simplificar para el caso univariado–.
Partamos de plantear: \[\begin{eqnarray} Vech(\hat{\mathbf{U}}_t \hat{\mathbf{U}}_t') & = & \mathbf{B}_0 + \mathbf{B}_1 Vech(\hat{\mathbf{U}}_{t-1} \hat{\mathbf{U}}_{t-1}') + \ldots \\ \nonumber & & + \mathbf{B}_q Vech(\hat{\mathbf{U}}_{t-q} \hat{\mathbf{U}}_{t-q}') + \varepsilon_t \tag{6.4} \end{eqnarray}\]
Dada la estimación en la ecuación (6.4), plantearemos la estructura de hipótesis dada por: \[\begin{eqnarray*} H_0 & : & \mathbf{B}_1 = \mathbf{B}_2 = \ldots = \mathbf{B}_q = 0 \\ H_a & : & No H_0 \end{eqnarray*}\]
La estadística de prueba será determinada por: \[\begin{equation} LM_{M-ARCH} = \frac{1}{2} T K (K + 1) - Traza \left( \hat{\Sigma}_{ARCH} \hat{\Sigma}^{-1}_{0} \right) \sim \chi^2_{[q K^2 (K + 1)^2 / 4]} \end{equation}\]
Donde la matriz \(\hat{\Sigma}_{ARCH}\) se calcula de acuerdo con la ecuación (6.4) y la matriz \(\hat{\Sigma}_{0}\) sin considerar una estructura dada para los errores.