4 Desestacionalización y filtrado de Series
4.1 Motivación
Existen múltiples enfoques para la desestacionalización de series. Algunos modelos, por ejemplo, pueden estar basados en modelos ARIMA como un conjunto de dummies. No obstante, en el caso partícular que discutiremos en este curso, estará basado en un modelo ARIMA de la serie. Este enfoque está basado en el modelo X11 de la oficina del censo de Estados Unidos (Census Bureau) el cual es conocido como el modelo X13-ARIMA-SEATS. El modelo X13-ARIMA-SEATS es, como su nombre lo indica, la combinación de un modelo ARIMA con componentes estacionales (por la traducción literal de la palabra: seasonal).
Un modelo ARIMA estacional emplea la serie en diferencias y como regresores los valores rezagados de las diferencia de la serie tantas veces como procesos estacionales \(s\) existan en ésta, con el objeto de remover los efectos aditivos de la estacionalidad. Sólo para entender qué significa este mecanismo, recordemos que cuando se utiliza la primera direncia de la serie respecto del periodo inmediato anterior se remueve la tendencia. Por su parte, cuando se incluye la diferencia respecto del mes \(s\) se está en el caso en que se modela la serie como una media móvil en términos del rezago \(s\).
El modelo ARIMA estacional incluye como componentes autoregresivos y de medias móviles a los valores rezagados de la serie en el periodo \(s\) en diferencias. El ARIMA(p, d, q)(P, D, Q) estacional puede ser expresado de la siguiente manera utilizando el operador rezago \(L\): \[\begin{equation} \Theta_P(L^s) \theta_p(L) (1 - L^s)^D (1 - L)^d X_t = \Psi_Q(L^s) \psi_q(L) U_t (\#eq:ARIMA_seas) \end{equation}\]
Donde \(\Theta_P(.)\), \(\theta_p(.)\), \(\Psi_Q(.)\) y \(\psi_q(.)\) son polinomios de \(L\) de orden \(P\), \(p\), \(Q\) y \(q\) respectivamente. En general, la representación es de una serie no estacionaria, aunque si \(D = d = 0\) y las raíces del polinomio carácteristico (de los polinomios del lado izquierdo de la ecuación @ref(eq:ARIMA_seas) todas son más grandes que 1 en valor absoluto, el proceso modelado será estacionario.
Si bien es cierto que existen otras formas de modelar la desestacionalización, como la modelación en diferencias con dummies para identificar ciertos patrones regulares, en los algorimtos disponibles como el X11 o X13-ARIMA-SEATS se emplea la formulación de la ecuación @ref(eq:ARIMA_seas). A continuación implementaremos la desestacionalización de una serie.
Como ejemplo utilizaremos la serie del Índice Nacional de Precios al Consumidor (INPC). Podemos ver que la serie original del INPC y su ajuste estacional bajo una metodología X13-ARIMA-SEATS son como se muestra en la Figura 4.1.
knitr::include_graphics("Plots/G_INPC_Adj.png") 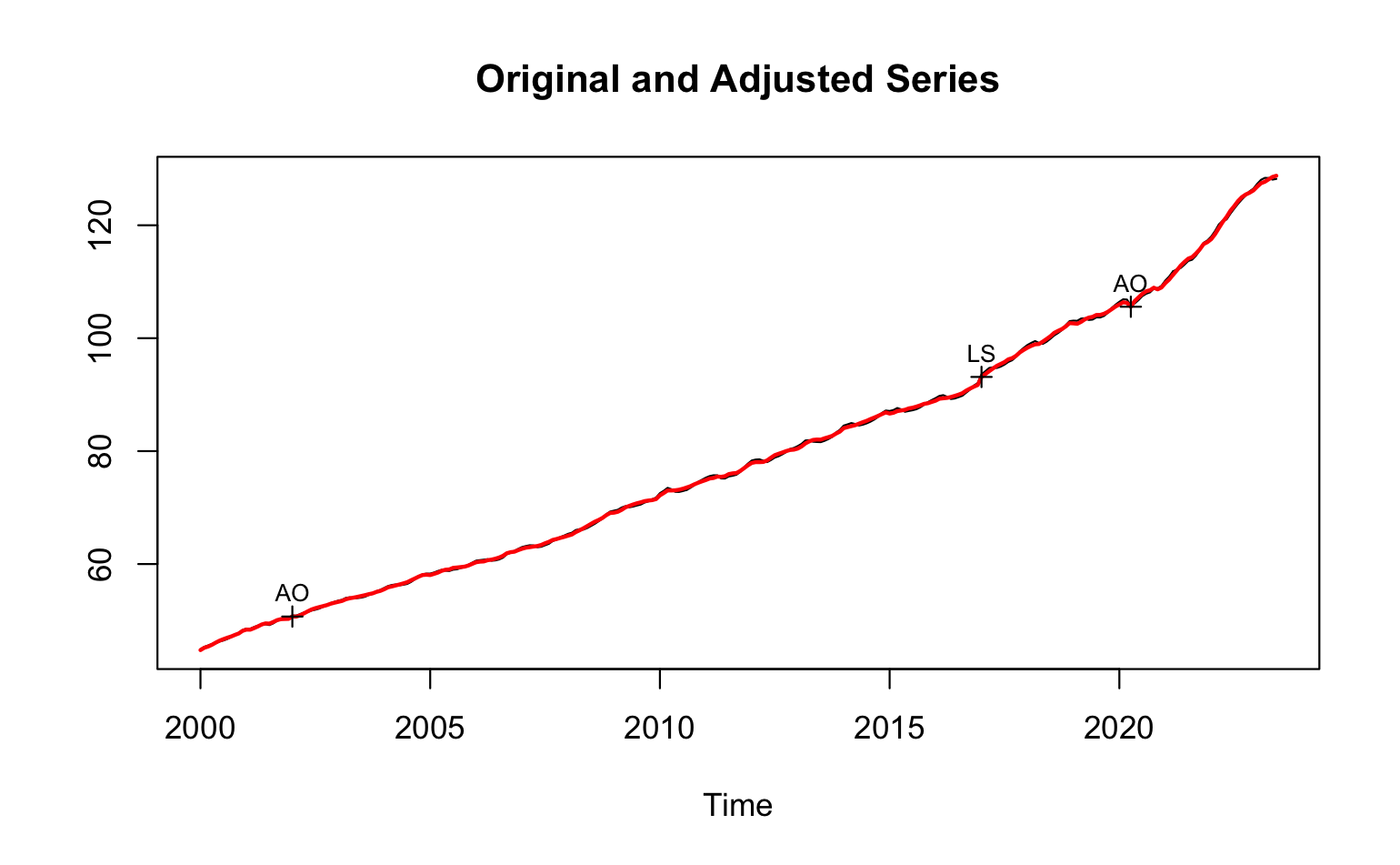
Figure 4.1: Índice Nacional de Precios al Consumidor (\(INPC_t\)) y su serie desestacionalizada utilizando un proceso X13-ARIMA-SEATS
4.2 Filtro Hodrick-Prescott
Como último tema de los procesos univariados y que no necesariamente aplican a series estacionarias, a continuación desarrollaremos el procedimiento conocido como filtro de Hodrick y Prescott (1997). El trabajo de estos autores era determinar una técnica de regresión que permitiera utilizar series agregadas o macroeconómicas para separarlas en dos componentes: uno de ciclo de negocios y otro de tendencia. En su trabajo orignal Hodrick y Prescott (1997) utilizaron datos trimestrales de alguna series como el Gross Domestic Product (GNP, por sus siglas enn Inglés), los agregados montearios M1, empleo, etc., de los Estados Unidos que fueron observados posteriormente a la Segunda Guerra Mundial.
El marco conceptual de Hodrick y Prescott (1997) parte de suponer una serie \(X_t\) que se puede descomponer en la suma de componente de crecimiento tendencial, \(g_t\), y su componente de ciclio de negocios, \(c_t\), de esta forma para \(t = 1, 2, \ldots, T\) tenemos que: \[\begin{equation} X_t = g_t + c_t (\#eq:HP_Eq) \end{equation}\]
En la ecuación @ref(eq:HP_Eq) se asume que el ajuste de la ruta seguida por \(g_t\) es resultado de la suma de los cuadrados de su segunda diferencia. En esa misma ecuación sumiremos que \(c_t\) son las desviaciones de \(g_t\), las cuales en el largo plazo tienen una media igual a cero (0). Por esta razón, se suele decir que el filtro de Hodrick y Prescott represeta una una descomposición de la serie en su componente de crecimiento natural y de sus desviaciones transitorias que en promedio son cero, en el largo plazo.
Estas consideraciones que hemos mencionado señalan que el procesimiento de Hodrick y Prescott (1997) implican resolver el siguiente problema minimización para determinar cada uno de los componentes en que \(X_t\) se puede descomponer: \[\begin{equation} \min_{\{ g_t \}^T_{t = -1} } \left[ \sum^T_{t = 1} c^2_t + \lambda \sum^T_{t = 1} [ \Delta g_t - \Delta g_{t-1}]^2 \right] \end{equation}\]
Donde \(\Delta g_t = g_t - g_{t-1}\) y \(\Delta g_{t-1} = g_{t-1} - g_{t-2}\); \(c_t = X_t - g_t\), y el parámetro \(\lambda\) es un número positivo que penaliza la variabilidad en el crecimiento de las series. De acuerdo con el trabajo de Hodrick y Prescott (1997) la constante \(\lambda\) debe tomar valores especificos de acuerdo con la periodicidad de la series. Así, \(\lambda\) será:En resumen, podemos decir que el filtro de Hodrick y Prescott (1997) es un algoritmo que mimiza las distancias o variaciones de la trayectoria de largo plazo. De esta forma, determina una trayectoria estable de largo plazo, por lo que las desviaciones respecto de esta trayectoria serán componentes de ciclos de negocio o cambios transitorios (tanto positivos como negativos).
A contiuación, ilustraremos el filtro de Hodrick y Prescott (1997) para dos series desestacionalizadas: \(INPC_t\) y \(TC_t\). Las Figura 4.2 y Figura 4.3 muestran los resultados de la implementación del filtro.
knitr::include_graphics("Plots/G_INPC_HP.png") 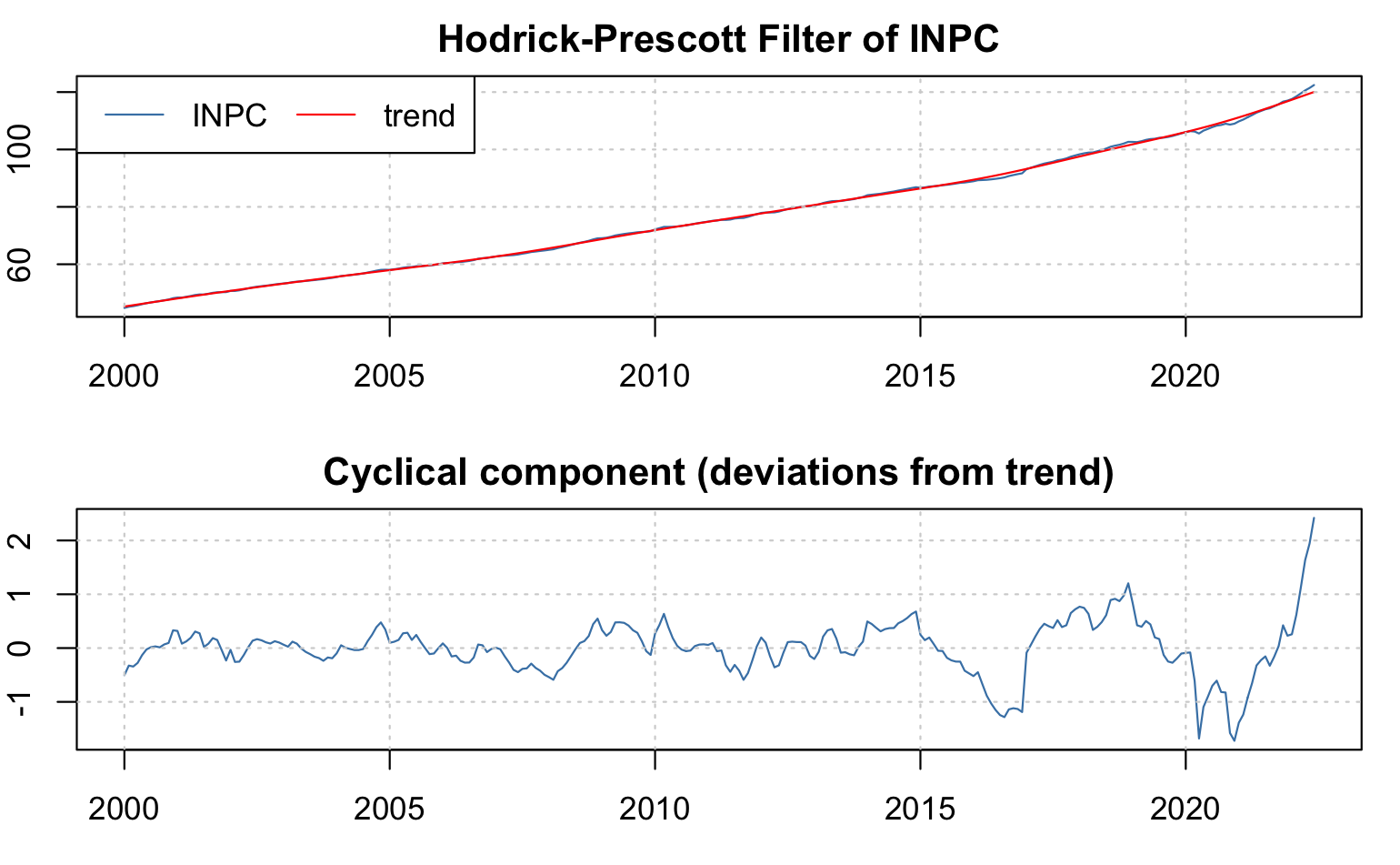
Figure 4.2: Descomposición del Índice Nacional de Precios al Consumidor (\(INPC_t\)) en su tendencia o trayectoria de largo plazo y su ciclo de corto plazo utilizando un filtro Hodrick y Prescott (1997)
knitr::include_graphics("Plots/G_TC_HP.png") 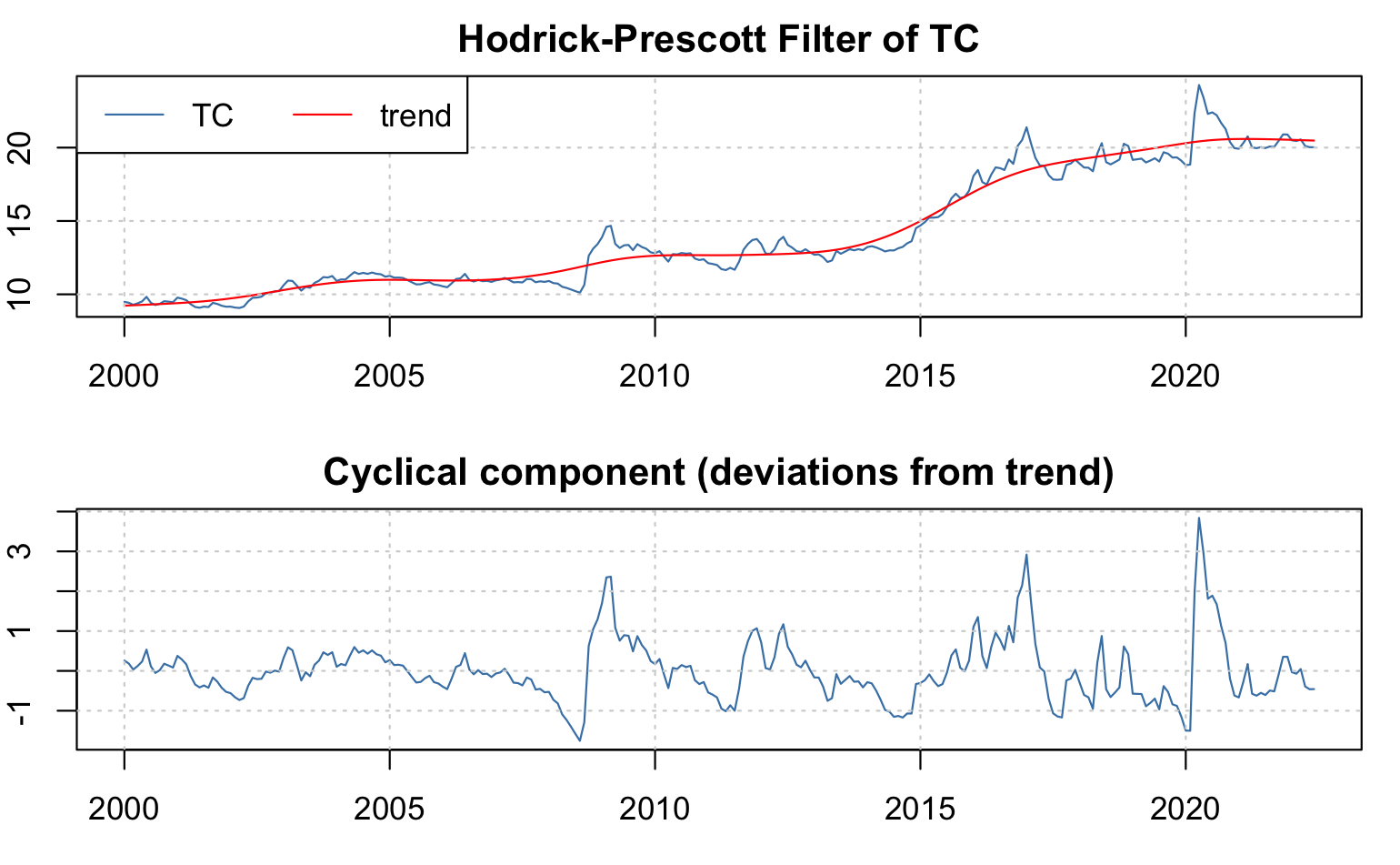
Figure 4.3: Descomposición del Tipo de Cambio FIX (\(TC_t\)) en su tendencia o trayectoria de largo plazo y su ciclo de corto plazo utilizando un filtro Hodrick y Prescott (1997)
4.2.1 Filtro Hodrick-Prescott planteado por St-Amant & van Norden
Método tradicional de HP consiste en minimizar la serie \(\{ \tau_t \}_{t=-1}^T\):
\[\sum_{t=1}^T (y_t - \tau_t)^2 + \lambda \sum_{t=1}^{T} [(\tau_{t} - \tau_{t-1}) - (\tau_{t-1} - \tau_{t-2})]^2\]
Donde \(\lambda\) es una parámetro fijo (determinado ex-ante) y \(\tau_t\) es un componente de tendencia de \(y_t\).
Sin pérdida de generalidad, asumiremos que \(\tau_{-1}\) y \(\tau_{0}\) son cero (0). De esta manera, la forma matricial del filtro HP es: \[(Y - G)'(Y - G) + \lambda G' K' K G\]
La derivada de los anteriores: \[-2 Y + 2 G + \lambda 2 K' K G = 0\]
Despejando: \[G_{hp} = [I_T + \lambda K' K]^{-1} Y\]
Donde \(G\) es el vector de tendencia, \(Y\) es el vector de la serie de datos, \(\lambda\) es la constante tradicional, y \(K\) es de dimensión \(T \times T\) y está dada por la expresión: \[K = \begin{pmatrix} 1 & 0 & 0 & 0 & \ldots & 0 \\ -2 & 1 & 0 & 0 & \ldots & 0 \\ 1 & -2 & 1 & 0 & \ldots & 0 \\ 0 & 1 & -2 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 1 \\ \end{pmatrix} \]
Así:
\[K' = \begin{pmatrix} 1 & -2 & 1 & 0 & \ldots & 0 \\ 0 & 1 & -2 & 1 & \ldots & 0 \\ 0 & 0 & 1 & -2 & \ldots & 0 \\ 0 & 0 & 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 1 \\ \end{pmatrix} \]
Método modificado de HP consiste en minimizar los valores de la serie \(\{ \tau_t \}_{t=1}^T\): \[\sum_{t=1}^T (y_t - \tau_t)^2 + \lambda \sum_{t=2}^{T-1} [(\tau_{t+1} - \tau_t) - (\tau_t - \tau_{t-1})]^2 + \lambda_{ss} \sum_{t=T-j}^{T} [\Delta \tau_t - u_{ss}]\]
Donde \(\lambda\) es una parámetro fijo (determinado ex-ante), \(\tau_t\) es un componente de tendencia de \(y_t\), y los nuevos parámetros son \(u_{ss}\) y \(\lambda_{ss}\) ajustadas por el procedimiento de Marcet y Ravn (2004).
Este procedimiento asume que parte del filtro HP y que esta versión tiene el problema de pérdida de información al final y al principio de la muestra. La razón es que es un procedimeinto univariado que requiere de mucha información futura y pasada para mejorar el ajuste.
El compoenente adicional al filtro HP es un componente de castigo por desviaciones de la tasa de crecimiento de largo plazo, \(u_{ss}\).
El proceso de selección de \(\lambda_{ss}\) es e propuesto por Marcet y Ravn (2004), el cual consiste en utilizar un \(\lambda\) convencional y el filtro HP convencional para estimar la siguiente función: \[F(\lambda) = \frac{\sum_{t=2}^{T-1} ((\tau_{t+1} - \tau_t) - (\tau_t - \tau_{t-1}))^2}{\sum_{t=1}^T (y_t - \tau_t)^2}\]
Entonces el valor de \(\lambda_{ss}\) será aquel que: \[F(\lambda_{ss}) = \frac{\sum_{t=2}^{T-1} ((\tau_{t+1} - \tau_t) - (\tau_t - \tau_{t-1}))^2}{\sum_{t=1}^T (y_t - \tau_t)^2} = F(\lambda)\]
nota: Antón (2009) estimó \(\lambda_{ss} = 1096\) para datos trimestrales del PIB.
La forma matricial del filtro HP-SAVN es: \[(Y - G)'(Y - G) + \lambda G' K' K G + \lambda_{ss} (L^j G + \overline{u}_{ss} M^j)\]
Donde \(L^j = (0, 0, \ldots, 0, -1, 0, \ldots, 0, 1)\), en el cual el valor \(-1\) es en la posición \(T-j-1\)-ésima, y \(M^j\) es un vector que toma valores de cero hasta antes de \(T-j\) y de 1 después.
La derivada de los anteriores: \[-2 Y + 2 G + \lambda 2 K' K G + \lambda_{ss} L'^j = 0\]
Despejando: \[G_{SAVN} = \frac{1}{2} [I_T + \lambda K' K]^{-1} (2 Y - \lambda_{ss} L'^j)\]
\[G_{SAVN} = [I_T + \lambda K' K]^{-1} Y - \frac{1}{2} [I_T + \lambda K' K]^{-1} \lambda_{ss} L'^j\]
Donde \(G\) es el vector de tendencia, \(Y\) es el vector de la serie de datos, \(\lambda\) es la constante tradicional, y \(K\) es de dimensión \(T \times T\) y está dada por la expresión:
\[K' = \begin{pmatrix} 1 & -2 & 1 & 0 & \ldots & 0 \\ 0 & 1 & -2 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 1 \\ \end{pmatrix} \]
Dicho lo anterior, podemos modificar \(F(\lambda)\) para el filtro HP convencional como en forma matricial: \[F(\lambda) = \frac{G' K' K G}{(Y - G)'(Y - G)}\]