8 Modelos ADRL

8.1 Teoría

Una vez que hemos analizado diversas técnicas de series de tiempo, el problema consiste en seleccionar el modelo correcto. La Figura 8.1 muestra un esquema o diagrama de cómo podríamos proceder para seleccionar el modelo correcto.

knitr::include_graphics("Plots/TimeSeries_Models.png")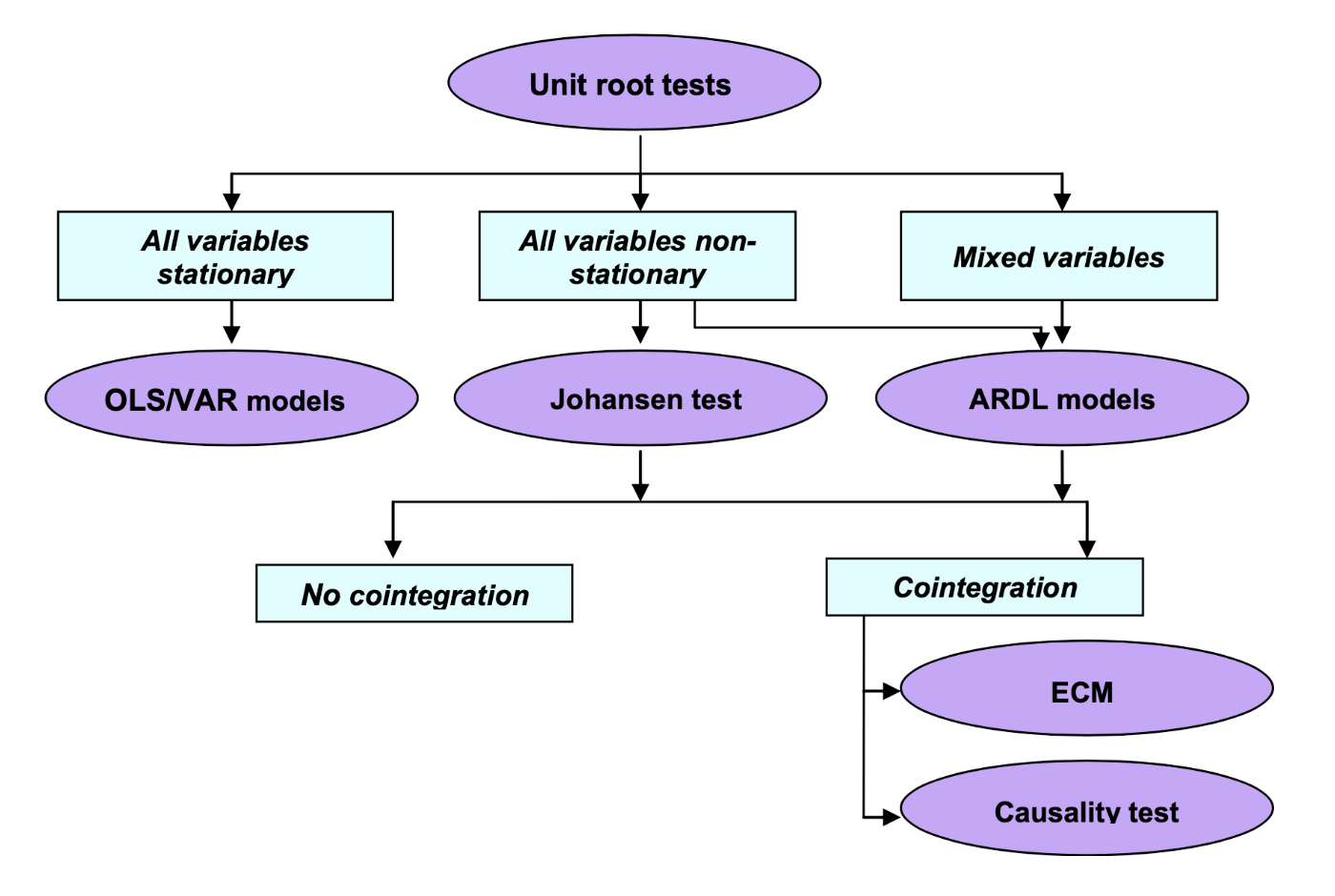 

Figure 8.1: Method selection for time series data. OLS: Ordinary least squares; VAR: Vector autoregressive; ARDL: Autoregressive distributed lags; ECM: Error correction models, retomado de: Shrestha y Bhatta (2018)

En este caso incorporaremos a los modelos autogregressive distributed lag models (ARDL, por sus siglas en inglés). En estos casos el procedimiento de Johansen no podría aplicarse directamennte cuando las variables incluidas son de un orden mixto o cuando simplemente todas no son estacionarias. Un modelo ARDL está basado en procedimientos de MCO.

Este tipo de modelos toma suficientes rezagos para capturar el mecanismo generador de datos. También es posible llegar a una especificación del mecanismo corrector de errores a partir de una trasformación lineal del ARDL.

Consideremos la siguiente ecuación: \[\begin{equation} Y_t = \alpha + \delta X_t + \gamma Z_t + U_t \tag{8.1} \end{equation}\]

Dada la ecuación (8.1) podemos establecer su forma de mecanismo corrector de errores en forma ARDL dada por: \[\begin{eqnarray*} \Delta Y_t & = & \alpha + \sum_{i = 1}^p \beta_i \Delta Y_{t-i} + \sum_{i = 1}^p \delta_i \Delta X_{t-i} + \sum_{i = 1}^p \gamma_i \Delta Z_{t-i} \\ & & + \lambda_1 Y_{t-1} + \lambda_2 X_{t-1} + \lambda_3 Z_{t-1} + U_t \end{eqnarray*}\]

Donde los coeficientes \(\beta_i\), \(\delta_i\), \(\gamma_i\) representan la dinámica de corto plazo y las \(\lambda\)’s la dinámica de largo plazo.

La hipótesis nula (\(H_0\)) es que las \(\lambda_1 + \lambda_2 + \lambda_3 = 0\), es decir, que no existe relación de largo plazo.

En la práctica estimamos una especificación con rezafos distribuidos: \[\begin{equation} Y_t = \alpha + \sum_{i = 1}^p \beta_i Y_{t-i} + \sum_{i = 1}^p \delta_i X_{t-i} + \sum_{i = 1}^p \gamma_i Z_{t-i} + U_t \end{equation}\]

Además de verificar si las series involucradas son estacionarias y decidir el número de reagos \(p\) mediante criterios de información.

8.2 Ejemplo

8.2.1 DESCRIPCIÓN DEL PROBLEMA

Supongamos que queremos modelar el logaritmo de dinero (M2) como una función de LRY (logarithm of real income), IBO (bond rate) e IDE (bank deposit rate).

• El problema es que la aplicación de una regresión de MCO en datos no estacionarios daría lugar a una regresión espúria.

• Los parámetros estimados serían consistentes solo si las series estuvieran cointegradas.

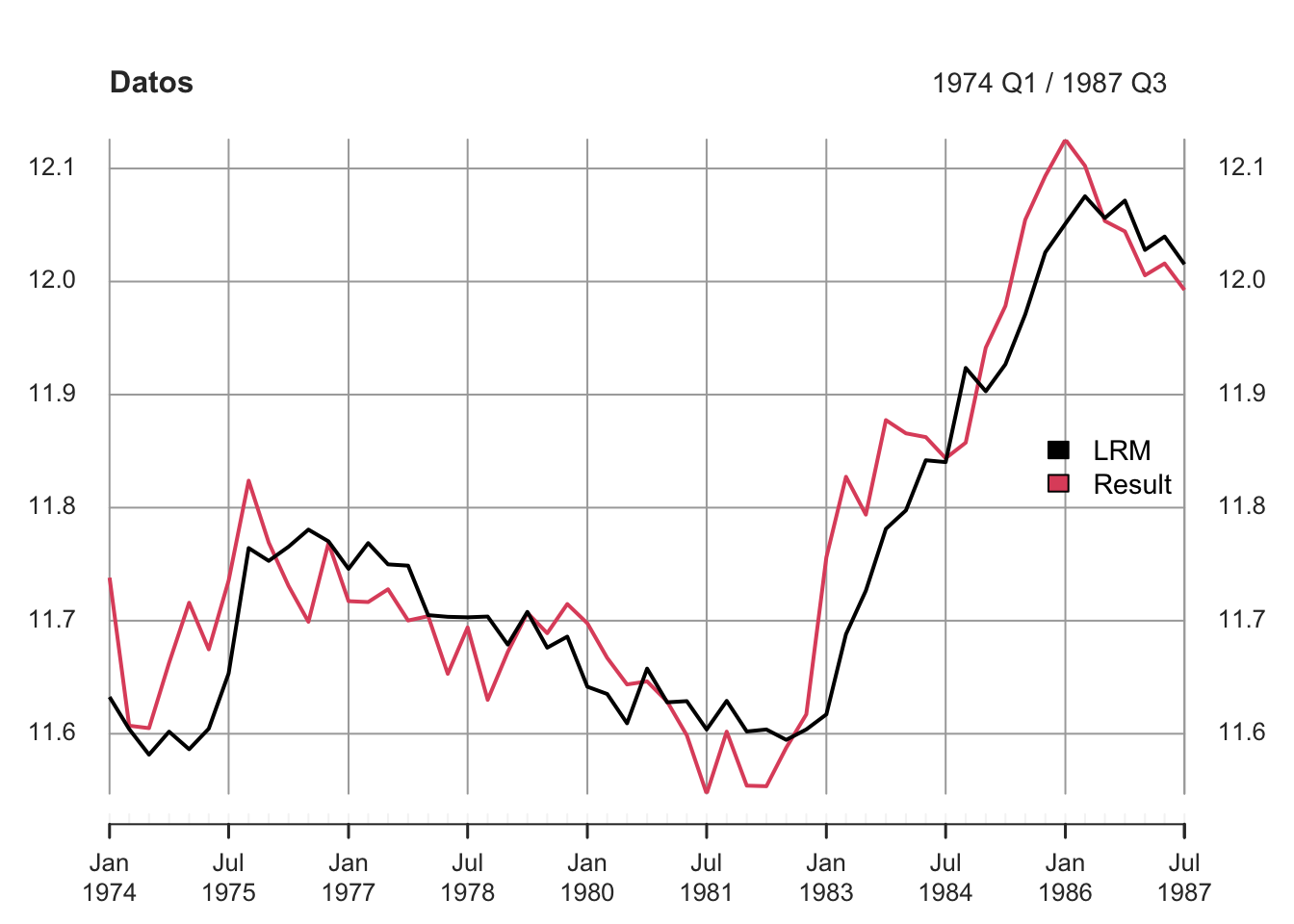
8.2.2 Importamos Datos desde un dataset de R:

A data frame with 55 rows and 5 variables. Time period from 1974:Q1 until 1987:Q3.

LRM: logarithm of real money, M2

LRY: logarithm of real income

LPY: logarithm of price deflator

IBO: bond rate

IDE: bank deposit rate

library(zoo) 
library(xts) 
library(ARDL)

#
data(denmark)

names(denmark)

## [1] "LRM" "LRY" "LPY" "IBO" "IDE"

8.2.3 Procedimiento:

1. Calculamos un auto ADRL para determinar la combinación óptima de rezagos.

models <- auto_ardl(LRM ~ LRY + IBO + IDE, data = denmark, max_order = 5)

names(models)

## [1] "best_model" "best_order" "top_orders"

#
models$top_orders

##    LRM LRY IBO IDE       AIC
## 1    3   1   3   2 -251.0259
## 2    3   1   3   3 -250.1144
## 3    2   2   0   0 -249.6266
## 4    3   2   3   2 -249.1087
## 5    3   2   3   3 -248.1858
## 6    2   2   0   1 -247.7786
## 7    2   1   0   0 -247.5643
## 8    2   2   1   1 -246.6885
## 9    3   3   3   3 -246.3061
## 10   2   2   1   2 -246.2709
## 11   2   1   1   1 -245.8736
## 12   2   2   2   2 -245.7722
## 13   1   1   0   0 -245.6620
## 14   2   1   2   2 -245.1712
## 15   3   1   2   2 -245.0996
## 16   1   0   0   0 -244.4317
## 17   1   1   0   1 -243.7702
## 18   5   5   5   5 -243.3120
## 19   4   1   3   2 -243.0728
## 20   4   1   3   3 -242.4378

#
models$best_order

## LRM LRY IBO IDE 
##   3   1   3   2

#
models$best_model

## 
## Time series regression with "zooreg" data:
## Start = 1974 Q4, End = 1987 Q3
## 
## Call:
## dynlm::dynlm(formula = full_formula, data = data, start = start, 
##     end = end)
## 
## Coefficients:
## (Intercept)    L(LRM, 1)    L(LRM, 2)    L(LRM, 3)          LRY    L(LRY, 1)  
##      2.6202       0.3192       0.5326      -0.2687       0.6728      -0.2574  
##         IBO    L(IBO, 1)    L(IBO, 2)    L(IBO, 3)          IDE    L(IDE, 1)  
##     -1.0785      -0.1062       0.2877      -0.9947       0.1255      -0.3280  
##   L(IDE, 2)  
##      1.4079

#
BestMod <- models$best_model

summary(BestMod)

## 
## Time series regression with "zooreg" data:
## Start = 1974 Q4, End = 1987 Q3
## 
## Call:
## dynlm::dynlm(formula = full_formula, data = data, start = start, 
##     end = end)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.029939 -0.008856 -0.002562  0.008190  0.072577 
## 
## Coefficients:
##             Estimate Std. Error t value   Pr(>|t|)    
## (Intercept)   2.6202     0.5678   4.615 0.00004187 ***
## L(LRM, 1)     0.3192     0.1367   2.336   0.024735 *  
## L(LRM, 2)     0.5326     0.1324   4.024   0.000255 ***
## L(LRM, 3)    -0.2687     0.1021  -2.631   0.012143 *  
## LRY           0.6728     0.1312   5.129 0.00000832 ***
## L(LRY, 1)    -0.2574     0.1472  -1.749   0.088146 .  
## IBO          -1.0785     0.3217  -3.353   0.001790 ** 
## L(IBO, 1)    -0.1062     0.5858  -0.181   0.857081    
## L(IBO, 2)     0.2877     0.5691   0.505   0.616067    
## L(IBO, 3)    -0.9947     0.3925  -2.534   0.015401 *  
## IDE           0.1255     0.5545   0.226   0.822161    
## L(IDE, 1)    -0.3280     0.7213  -0.455   0.651847    
## L(IDE, 2)     1.4079     0.5520   2.550   0.014803 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0191 on 39 degrees of freedom
## Multiple R-squared:  0.988,  Adjusted R-squared:  0.9843 
## F-statistic: 266.8 on 12 and 39 DF,  p-value: < 0.00000000000000022

2. UECM (Unrestricted Error Correction Model) of the underlying ARDL.

UECM_BestMod <- uecm(BestMod)

summary(UECM_BestMod)

## 
## Time series regression with "zooreg" data:
## Start = 1974 Q4, End = 1987 Q3
## 
## Call:
## dynlm::dynlm(formula = full_formula, data = data, start = start, 
##     end = end)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.029939 -0.008856 -0.002562  0.008190  0.072577 
## 
## Coefficients:
##              Estimate Std. Error t value   Pr(>|t|)    
## (Intercept)   2.62019    0.56777   4.615 0.00004187 ***
## L(LRM, 1)    -0.41685    0.09166  -4.548 0.00005154 ***
## L(LRY, 1)     0.41538    0.11761   3.532    0.00108 ** 
## L(IBO, 1)    -1.89172    0.39111  -4.837 0.00002093 ***
## L(IDE, 1)     1.20534    0.44690   2.697    0.01028 *  
## d(L(LRM, 1)) -0.26394    0.10192  -2.590    0.01343 *  
## d(L(LRM, 2))  0.26867    0.10213   2.631    0.01214 *  
## d(LRY)        0.67280    0.13116   5.129 0.00000832 ***
## d(IBO)       -1.07852    0.32170  -3.353    0.00179 ** 
## d(L(IBO, 1))  0.70701    0.46874   1.508    0.13953    
## d(L(IBO, 2))  0.99468    0.39251   2.534    0.01540 *  
## d(IDE)        0.12546    0.55445   0.226    0.82216    
## d(L(IDE, 1)) -1.40786    0.55204  -2.550    0.01480 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0191 on 39 degrees of freedom
## Multiple R-squared:  0.7458, Adjusted R-squared:  0.6676 
## F-statistic: 9.537 on 12 and 39 DF,  p-value: 0.00000003001

3. RECM (Restricted Error Correction Model) of the underlying ARDL Obs: allowing the constant to join the short-run relationship (case 2), instead of the long-run (case 3)

RECM_BestMod <- recm(UECM_BestMod, case = 2)

summary(RECM_BestMod)

## 
## Time series regression with "zooreg" data:
## Start = 1974 Q4, End = 1987 Q3
## 
## Call:
## dynlm::dynlm(formula = full_formula, data = data, start = start, 
##     end = end)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.029939 -0.008856 -0.002562  0.008190  0.072577 
## 
## Coefficients:
##              Estimate Std. Error t value    Pr(>|t|)    
## d(L(LRM, 1)) -0.26394    0.09008  -2.930    0.005405 ** 
## d(L(LRM, 2))  0.26867    0.09127   2.944    0.005214 ** 
## d(LRY)        0.67280    0.11591   5.805 0.000000703 ***
## d(IBO)       -1.07852    0.30025  -3.592    0.000837 ***
## d(L(IBO, 1))  0.70701    0.44359   1.594    0.118300    
## d(L(IBO, 2))  0.99468    0.36491   2.726    0.009242 ** 
## d(IDE)        0.12546    0.48290   0.260    0.796248    
## d(L(IDE, 1)) -1.40786    0.48867  -2.881    0.006160 ** 
## ect          -0.41685    0.07849  -5.311 0.000003633 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01819 on 43 degrees of freedom
##   (0 observations deleted due to missingness)
## Multiple R-squared:  0.7613, Adjusted R-squared:  0.7113 
## F-statistic: 15.24 on 9 and 43 DF,  p-value: 0.00000000009545

4. long-run levels relationship (cointegration)

bounds_f_test(BestMod, case = 2)

## 
##  Bounds F-test (Wald) for no cointegration
## 
## data:  d(LRM) ~ L(LRM, 1) + L(LRY, 1) + L(IBO, 1) + L(IDE, 1) + d(L(LRM,     1)) + d(L(LRM, 2)) + d(LRY) + d(IBO) + d(L(IBO, 1)) + d(L(IBO,     2)) + d(IDE) + d(L(IDE, 1))
## F = 5.1168, p-value = 0.004418
## alternative hypothesis: Possible cointegration
## null values:
##    k    T 
##    3 1000

5. Long-run multipliers (with standard errors, t-statistics and p-values)

multipliers(BestMod)

##          Term   Estimate Std. Error   t value           Pr(>|t|)
## 1 (Intercept)  6.2856579  0.7719160  8.142930 0.0000000006107445
## 2         LRY  0.9964676  0.1239310  8.040503 0.0000000008358472
## 3         IBO -4.5381160  0.5202961 -8.722180 0.0000000001058619
## 4         IDE  2.8915201  0.9950853  2.905801 0.0060092393605960

#
Result <- coint_eq(BestMod, case = 2)

8.2.4 Make the plot

Datos <- cbind.zoo(LRM = denmark[,"LRM"], Result)

Datos <- xts(Datos)

plot(Datos, legend.loc = "right")

Figure 8.2: Gráfica de la ecuación de cointegración